par J.C. Maurin, Professeur agrégé de physique
Afin d’élaborer les indicateurs de température, on utilise des radiomètres MSU, AMSU ou ATMS embarqués sur des satellites, puis on construit l’indicateur à partir des mesures et de diverses corrections. On obtient ainsi un indicateur qui concerne la quasi-totalité du globe, contrairement aux indicateurs terrestres basés essentiellement (avant 1980) sur quelques milliers de stations américaines et européennes. Au sujet des mesures par satellites, et sans être spécialiste dans ce domaine, un physicien peut néanmoins donner quelques éléments d’appréciation qu’ignore parfois un lecteur intéressé par la climatologie. Le but de la seconde partie de l’article sera atteint si ce lecteur a appris des éléments nouveaux, il pourra ensuite approfondir la question par lui-même.
Partie 1 de l’article ici.
3. Les mesures des radiomètres
Les instruments [4] MSU (Microwave Sounding Unit) AMSU (depuis 2000) et ATMS sont sensibles à la luminance énergétique (W⋅sr–1⋅m–2) dans la direction visée par l’antenne. Les instruments sont initialement destinés à la prévision météorologique et non à des études climatiques.
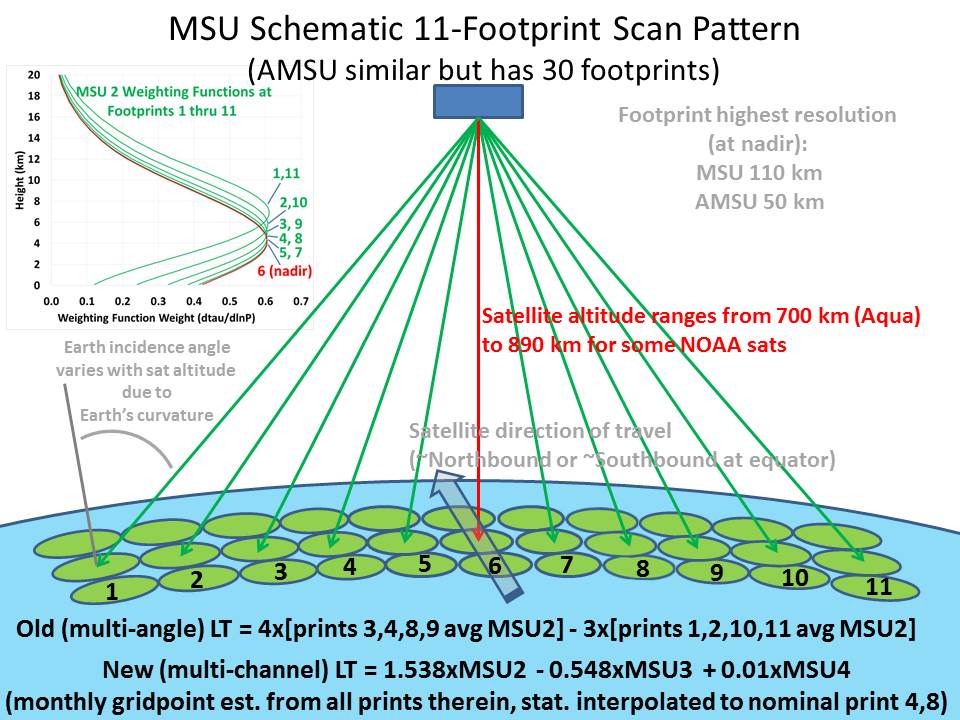
Figure 5a. [2] [4] L’échantillonnage spatial pour MSU. Une mesure individuelle (suivant un angle ≈ 7° fixé par l’antenne) porte sur une colonne d’air dont l’empreinte au sol ≈ 22 000 km² (2500 km² pour AMSU). Les mesures lors d’un balayage sont effectuées en une dizaine de secondes [3].
Dans l’idéal le radiomètre n’est sensible qu’à la luminance dans l’angle solide visé. En réalité les lobes latéraux d’antenne vont provoquer un biais de balayage (ici Fig.4). Les détecteurs sont le siège d’un bruit de mesure. NET (Noise équivalent Température) ≈ 0.25 K voir ici ou ici.
3.1. Elaboration de la « température » à partir de la luminance
On va déduire des mesures de luminance une température de brillance [5] pour certaines fréquences (entre 50 et 60 GHz, soit 5 à 6 µm, pour l’oxygène atmosphérique). La température de brillance est la température de rayonnement du corps noir qui délivre la même luminance énergétique L(ν) autour d’une fréquence ν particulière. C’est seulement dans ce cas idéal, que la température de brillance se déduit directement de la loi de Planck.
Dans le monde réel, la luminance L(ν), mesurée à 800 km d’altitude par les instruments MSU ou AMSU, est fonction de l’émission (B) et de l’absorption (τ) qui dépendent de la pression (altitude z), de la température T et de la fréquence ν. Mais on doit ajouter d’autres contributions très délicates à estimer.
Soit une expression du type

Les autres contributions (effets de surface, nuages) diminuent en très haute altitude → elles concernent donc moins l’indicateur TLS que l’indicateur TLT (voir fig. 5b). On peut surtout les minimiser par un choix judicieux de la fréquence ν.
La connaissance des paramètres physiques, le long de la ligne de visée et au moment de la mesure, doit permettre de résoudre le « problème inverse » c’est-à-dire remonter vers la température T à partir de L(ν) (voir ici). On utilise des fonctions de pondération théoriques qui modélisent une atmosphère standard. La « température » à l’altitude z, élaborée à partir des mesures de luminance, est donc une mesure indirecte, en tout cas, bien moins directe que celle obtenue avec une sonde de platine embarquée sur un ballon.
3.2 Les fonctions de pondération
Dans une seconde étape, RSS [1] et UAH [2] vont ensuite combiner plusieurs canaux (dont le canal 5) et plusieurs angles de visée pour remonter vers la « température » TLT (≈ 3.5 km). L’indicateur TLS (≈ 18 km) va utiliser surtout le canal 9. Des mesures directes de température par ballons permettent un certain étalonnage. On peut noter que l’influence de la surface conduit à 2 pondérations différentes (Land/Océan de la Fig.5b) pour le seul indicateur TLT. Mais plusieurs pondérations de type ’Land’ seraient nécessaires → concernant la réflexion du rayonnement, une zone humide sur un continent (Land) est plus proche de l’océan que du désert.
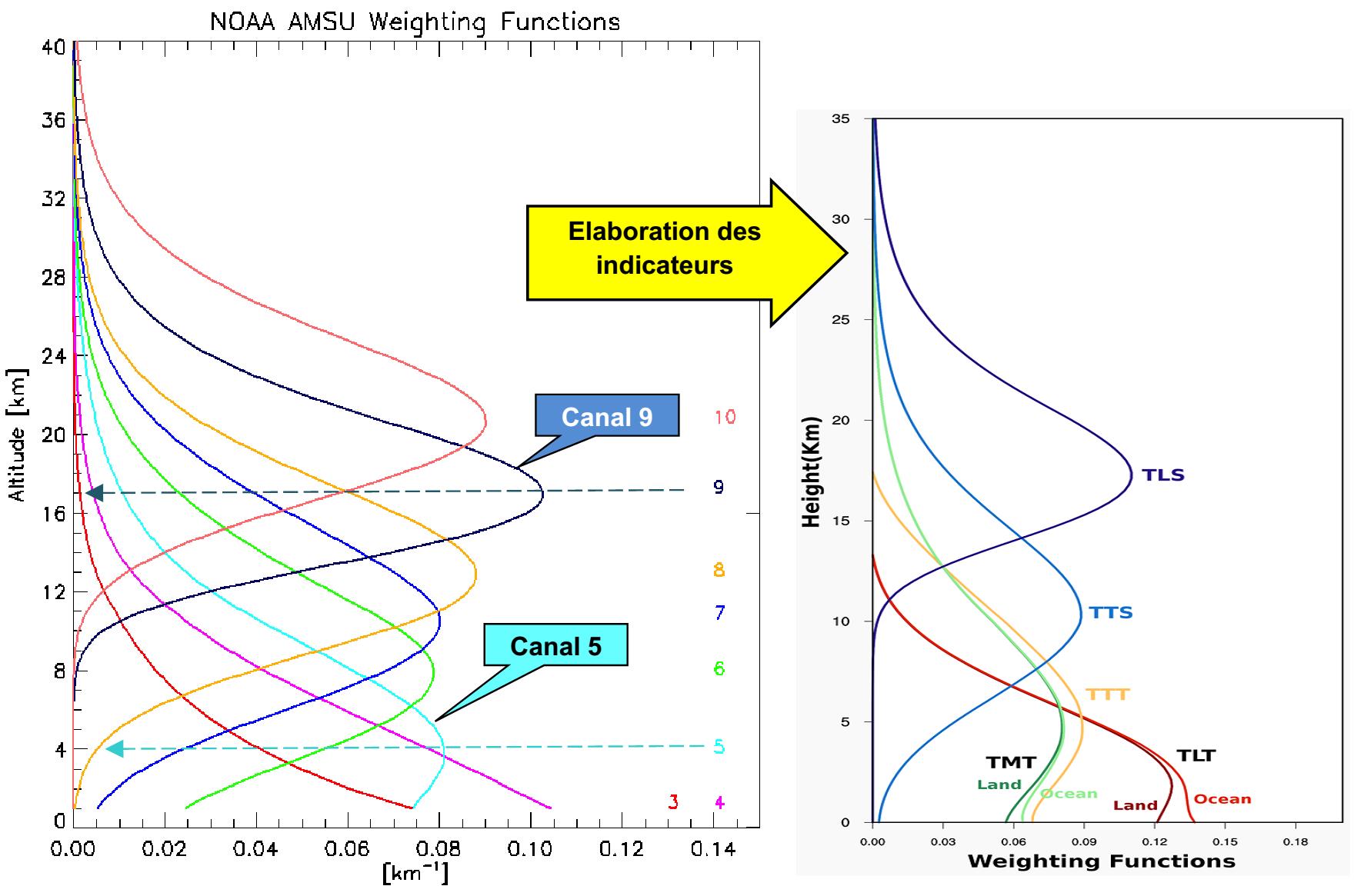
Figure 5b. Fonctions de pondération AMSU pour une observation au nadir (angle zéro) (ici ou ici).Les fonctions de pondération modélisent une atmosphère terrestre standard suivant l’angle de visée et le canal (fréquence ν).
Exemple pour le canal 5 (53,6 GHz) :
Au-dessous de 4 km l’absorption augmente plus vite que l’émission alors qu’au-dessus de 4 km l’émission diminue plus vite que l’absorption → la fonction de pondération sera maximale à l’altitude ≈ 4 km pour le canal 5. A partir de la luminance dans le canal 5, on déduit une « température moyenne » autour de 4 km d’altitude.
3.3 Les fréquences utilisées
Idéalement, la mesure de luminance devrait concerner la seule colonne d’air, entre la surface terrestre et le satellite à ≈ 800 km d’altitude. Mais les contributions de la surface terrestre, des nuages, de la vapeur d’eau etc. vont gêner la mesure. Pour limiter cette gêne, on utilise souvent l’oxygène (représentatif de la température de l’air) en considérant les canaux 3 à 14 (pour AMSU). Les canaux 5, 7 et 9 AMSU sont étroitement associés aux canaux 2, 3 et 4 de MSU.
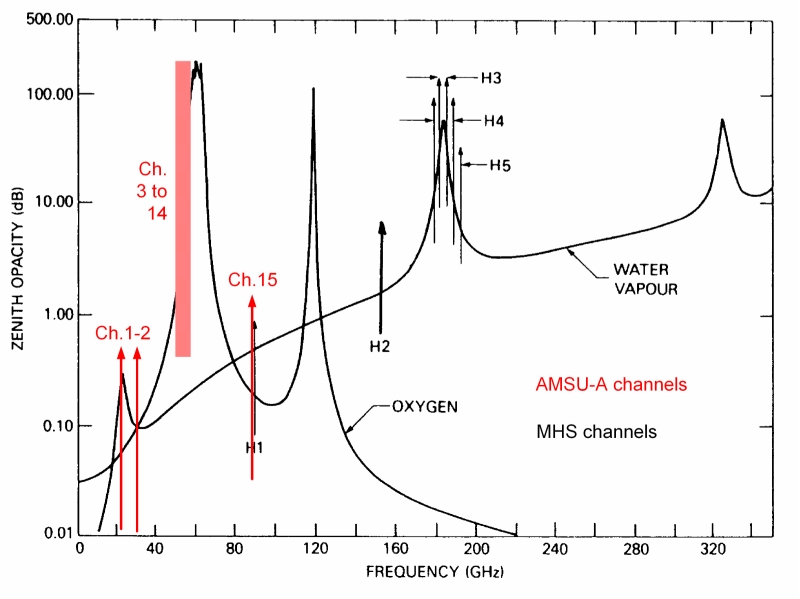 Figure 5c. Les fréquences pour AMSU voir ici.
Figure 5c. Les fréquences pour AMSU voir ici.
3.4 Remarques sur les mesures
• C’est seulement pour le corps noir que la luminance ne dépend que de la température. Les températures de brillance obtenues sont presque équivalentes à une moyenne de « température » d’une atmosphère standard pondérée verticalement. Mais il faut que la mesure (à 800 km d’altitude) soit indépendante (ou parfaitement corrigée) des autres grandeurs variables (pression, taux d’humidité, couverture nuageuse, effets de surface, etc.). La variation UAH/RSS pour TLT est inférieure à 0.2%, on peut donc s’interroger:
La répartition verticale de l’eau atmosphérique est-elle identique pour les années 1980 et 2010 ? Les fonctions de pondération sont-elles parfaitement constantes dans le temps ?
La pondération TLT au-dessus des continents est-elle similaire pour un désert, une forêt tropicale, une zone humide ?
• A la fin des années 90 il y a changement progressif de l’instrumentation: on passe des capteurs MSU vers AMSU (ici slide 3). Les instruments AMSU sont similaires aux MSU, mais ils effectuent des mesures en utilisant un plus grand nombre de canaux → les fréquences sont donc légèrement différentes. La taille des empreintes au sol est plus petite pour AMSU → le biais de balayage change. La différence pour la « température » entre MSU et AMSU dépasse parfois 1K (ici Fig.7). On peut noter un désaccord (Fig.3a du 1/2) entre RSS et UAH plus important à partir du changement d’instrumentation de la fin des années 90.
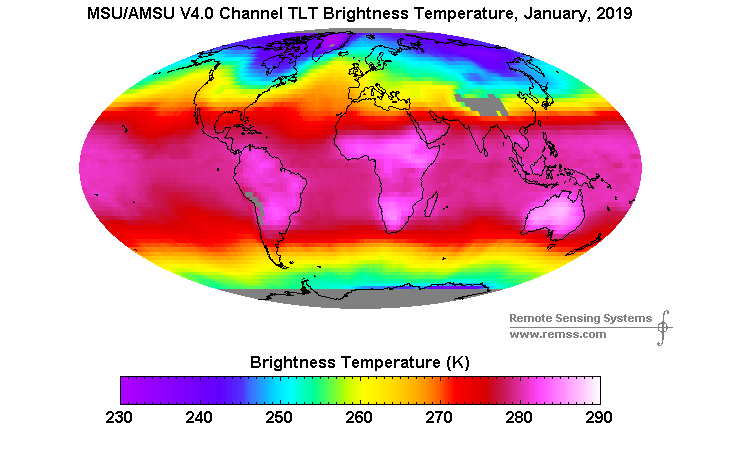 Figure 5d. Carte des températures TLT selon RSS (ici). Les températures de brillance déduites sont comprises entre 230 K et 290 K, soit une variabilité spatiale ≈ 60/265 = 23% contre 50% pour les températures au sol. On combine les mesures afin d’élaborer une moyenne sur ≈ 95 % de la surface terrestre. Les zones polaires et la très haute montagne (Himalaya, Andes) ne sont pas prises en compte.
Figure 5d. Carte des températures TLT selon RSS (ici). Les températures de brillance déduites sont comprises entre 230 K et 290 K, soit une variabilité spatiale ≈ 60/265 = 23% contre 50% pour les températures au sol. On combine les mesures afin d’élaborer une moyenne sur ≈ 95 % de la surface terrestre. Les zones polaires et la très haute montagne (Himalaya, Andes) ne sont pas prises en compte.
4. Les corrections [3].
On utilise plusieurs radiomètres, sur des satellites qui n’ont pas tous ni la même altitude ni la même vitesse. Les corrections à appliquer pour remonter vers une « température » seront donc différentes. Les instruments n’ont pas un étalonnage parfaitement stable et sont l’objet au cours des décennies de défaillances de canal. Les satellites supportant les instruments ont des orbites changeantes au fil du temps. Aucun radiomètre n’a mesuré en continu sur 4 décennies: depuis 1979, on a utilisé 15 satellites avec diverses durées de fonctionnement (ici slide 17/18), avec un calibrage légèrement différent, nécessitant une intercalibration entre satellites (ici Fig.1).
MSU et AMSU ont des fréquences de canal légèrement différentes → les fonctions de pondération changent. Les plates-formes satellites ont des orbites qui dérivent : les radiomètres observent donc à des heures locales différentes selon les années.
Tous les ajustements nécessaires impliquent des décisions concernant la méthodologie, et des méthodologies différentes aboutissent à des résultats différents pour RSS et UAH.
Une correction particulièrement délicate (correction diurne) concerne l’heure locale d’observation : la même empreinte au sol mesurée par exemple à 8H00 locale ou à 8H20 locale ne va pas donner la même température de brillance, et l’écart n’est pas négligeable. Cet écart dépend du moment de la journée, de la saison, de la géographie (continent, océan, désert, forêt, haute montagne, etc.). Les capacités thermiques font que la correction diurne est faible au-dessus des océans mais importante au-dessus des continents. 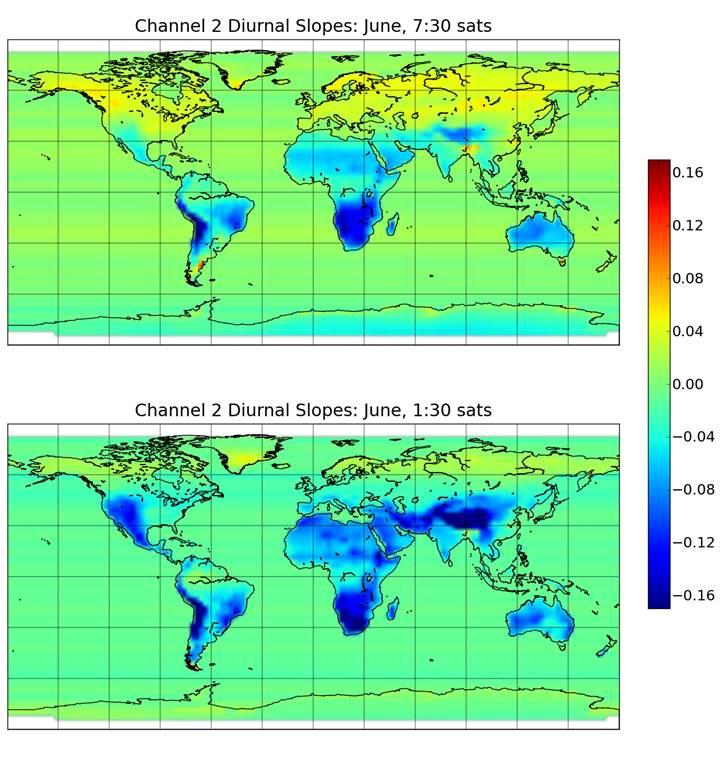 Figure 6. [2] Un exemple des corrections diurnes. Elles sont importantes au-dessus des continents. Suivant l’heure locale et la saison les corrections changent.
Figure 6. [2] Un exemple des corrections diurnes. Elles sont importantes au-dessus des continents. Suivant l’heure locale et la saison les corrections changent.
En pratique les corrections utilisent parfois des modèles théoriques (Community Climate Model → ici) ). En conséquence, le calcul des incertitudes n’est pas usuel, on est conduit à utiliser une méthode Monte-Carlo (voir ici) pour obtenir une estimation → (incertitude ≈ 0.1K ?). Pas moins d’une dizaine de versions pour chaque indicateur RSS/UAH se sont succédé depuis 1992. La dernière version (RSS 4.0 publiée en 2017) entraîne, presque à elle-seule, l’écart de 0.2 K entre RSS et UAH.
5. Remarques
• L’indicateur TLT ne correspond qu’à une fraction de l’atmosphère dont la partie supérieure (indicateur TLS) s’est faiblement refroidie (ici Figs 5/6). L’indicateur TLS (≈ 18 km) est a priori plus fiable car moins dépendant des autres contributions (surface, nuages) que l’indicateur TLT (≈3.5 km).
• Les océanographes ont documenté des cycles de l’ordre de ≈ 60 ans pour les océans (à partir d’observations sur la banquise nord, sur les températures, sur la vitesse de montée des océans, mais aussi sur le contenu thermique de l’océan). Sur quelques décennies, l’océan va impacter la basse atmosphère située au-dessus car la capacité thermique de l’océan est au moins 10 fois supérieure à celle de l’atmosphère (suivant la fraction d’océan concernée → voir Fig. 1 du 1/2). La tendance au-dessus de l’océan peut, pour partie, être la conséquence d’un cycle océanique naturel de 60 ans.
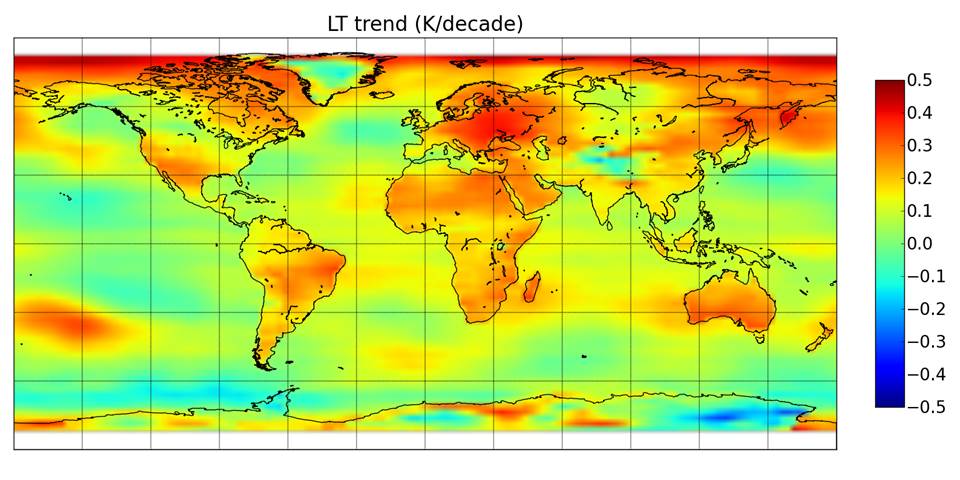 Figure 7. [2] Carte des tendances 1979 – 2015 selon UAH. La tendance (LT trend) à la hausse est plus grande au-dessus des continents qu’au-dessus de l’océan.
Figure 7. [2] Carte des tendances 1979 – 2015 selon UAH. La tendance (LT trend) à la hausse est plus grande au-dessus des continents qu’au-dessus de l’océan.
Les indicateurs RSS/UAH donnent pour la basse atmosphère une tendance moyenne ≈ 0.16 K/décennie. Mais cette tendance globale est surtout causée par les fortes valeurs au-dessus des continents (Fig.7), et nous avons vu (Fig. 6) que les corrections les plus notables sont justement les corrections diurnes pour les continents. Par ailleurs, bien qu’un désert soit différent d’une zone humide, l’indicateur TLT utilise une unique pondération (fig.5b) au-dessus des continents. A propos de la hausse des températures sur les seuls continents, on peut consulter ceci.
6. Conclusions
- On ne peut pas donner un sens physique précis à une «moyenne des températures de la basse atmosphère ». Pour tenter néanmoins de caractériser l’évolution thermique de la basse atmosphère, on utilise depuis 1979 des indicateurs satellites TLT qui sont des objets mathématiques basés sur des mesures indirectes.
- Sous l’influence de l’OMM, (co-créateur du GIEC), on a étendu à 100% du globe (et on remonte à 1850!) un indicateur terrestre qui ne devrait concerner que 5% de la surface (USA Europe Chine Japon) et seulement à partir de 1950 [6]. Depuis 1979, les indicateurs par satellites permettent d’avoir enfin un indicateur de température véritablement mondial. Ils présentent donc un net progrès par rapport aux indicateurs terrestres (voir ici). Ce progrès, important sur l’échantillonnage spatial, reste faible pour l’échantillonnage temporel.
- Les mesures par satellites comportent un changement d’instrumentation (MSU vers AMSU) à la fin des années 90. On utilise une procédure complexe de calcul et d’étalonnage, notamment pour les corrections diurnes au-dessus des continents qui dépendent parfois de modèles théoriques. Comment alors calculer une marge d’erreur ?
- Pour la basse atmosphère, la hausse en 40 ans des indicateurs RSS/UAH est ≈ 0.5 K, soit un changement relatif ≈ 0.2%. Les mesures indirectes [5] concernent des températures variant spatialement ≈ 20% et temporellement ≈ 20% (soit 100 fois le changement relatif de 0.2%).
- La hausse des indicateurs RSS/UAH ≈ +0.5 K doit être mise en regard avec la variabilité mensuelle (écart type ≈ 0.1K, valeur crête à crête ≈ 0.7K), avec les transitoires naturels > 0.5 K de type El Niño et avec le désaccord ≈ 0.2 K entre RSS et UAH.
- Entre la basse atmosphère et la haute atmosphère, les très faibles variations (0.2%) ont un sens opposé. Pour expliquer la légère hausse des indicateurs, le GIEC et son organisme fondateur l’OMM invoquent l’existence d’un «effet de serre» (voir ici) , mais il existe d’autres hypothèses (voir ici). Une partie de cette hausse peut (au-dessus des océans) être la conséquence de cycles océaniques naturels.
Références
1 Elaboration RSS http://www.remss.com/measurements/upper-air-temperature/
http://images.remss.com/papers/rsspubs/Mears_JTECH_2009_TLT_construction.pdf
2 Elaboration UAH http://www.drroyspencer.com/2015/04/version-6-0-of-the-uah-temperature-dataset-released-new-lt-trend-0-11-cdecade/
3 Corrections https://journals.ametsoc.org/doi/10.1175/JCLI-D-16-0768.1#
http://images.remss.com/papers/msu/MSU_AMSU_C-ATBD.pdf
https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2008JD011267
4 Instrumentation Satellite Microwave Sounding System: Past, Present and Futurei
Performances pour ATMS
5 Données MSU https://disc1.gesdisc.eosdis.nasa.gov/data/msu/MSULTT.001/
6 Indicateurs terrestres Fig.1 ici ou là
https://www.ncdc.noaa.gov/monitoring-references/docs/peterson-vose-1997.pdf
https://www.portoconference2018.org/uploads/1/1/7/3/117342822/5._limburg.pptx
https://journals.ametsoc.org/doi/pdf/10.1175/2011BAMS3124.1
https://www.rossmckitrick.com/temperature-data-quality.html
Merci, professeur Maurin, de cette intéressante prolongation de votre article 1 !
Vos conclusions offrent ici un recadrage tout en nuances p.r. aux avis (gratuits?) de certains commentateurs.
Il me semble ainsi que l’avenir thermique de notre globe échappe encore largement à ladite « certitude » d’idéologues et d’activistes qui le prédisent sombre, voire fort angoissant, noyant nos médias « grand public » et nos décideurs politiques sous de bien subtiles fake news ! D’où un toujours nécessaire questionnement sur ce qui influence réellement ce futur climatique en le dégageant d’esbroufe manipulatrice…
QUI influence QUI et QUOI ? (causes – origines – effets prospectifs), une éternelle Q. !
Après vos deux articles, une question me hante. Il s’agit des influences climatiques respectives : « soleil versus volcanisme ». Quelles seraient – comparativement – les puissances de leurs rayonnements thermiques? Dont celle liée aux masses de magma libérées par nos volcans terrestres (env. 1.500 ?) plus ceux sous-marins et failles estimées à 1.500.000, mais encore si peu explorées? La volcanologie n’étant pas ma discipline, je me suis donc mis en recherche de sources. Dont ici celle d’un géologue et de chiffres communément admis. Ils constituent un plaidoyer en faveur p.ex. de la géothermie. Sans qu’il soit ici mentions de rentabilités comparées entre technologies de mise en œuvre et d’échéances de mise en place.
Intéressant, car liant aussi nos océans et l’atmosphère !
……………………………………………………………………………………….
Pierre Thomas – ENS Lyon – Laboratoire de Géologie de Lyon
http://planet-terre.ens-lyon.fr/article/chaleur-Terre-geothermie.xml
dont quelques extraits qui suivent :
[[ Pour apprécier ce que représentent les puissances fournies par la Terre, il faut des points de comparaisons. La surface de la planète Terre reçoit en permanence 174.000 TW du Soleil (1,74.1017 W), ce qui correspond à une énergie de 5,5.1024 J par an. Cela revient à environ 1000 W.m-2 en plein soleil, et à une moyenne jour-nuit, été-hiver, pôles-équateur de 342 W.m-2.
La puissance totale produite et consommée par l’humanité (combustibles fossiles, nucléaire, énergies renouvelables…) pour tous ses besoins est d’environ 15 TW (15.1012 W), soit environ 5.1020 J par an (chiffre de 2010), ce qui correspond à environ 1/10.000 de ce que la Terre reçoit du soleil. ]] ….
[[ Un volcan, ça fume et ça chauffe ! La puissance (moyennée sur plusieurs années) dégagée par l’ensemble des éruptions volcaniques de notre planète semble énorme : environ 1 TW, soit la puissance fournie par 1.000 tranches de centrales nucléaires « usuelles ». La puissance moyenne dégagée par les séismes (puissance principalement mécanique, thermique et potentielle gravitationnelle) est mal connue, mais sans doute du même ordre de grandeur.
Mais ces 2 TW volcaniques et sismiques ne sont que la partie émergée de l’iceberg. ]]
[[ La Terre perd donc globalement 46 TW, ( puissance rayonnée vers l’espace ) dont 4% de manière spectaculaire (séismes et éruptions volcaniques) et 96% de manière très discrète (le flux géothermique). ]]
[[ On peut comparer ces 46 TW dégagés par la Terre aux 15 TW produits et consommés par l’humanité et aux 174.000 TW reçus du Soleil : la Terre ne dégage que 3 fois ce que produit/consomme l’humanité, mais environ 4.000 fois moins que ce qu’elle reçoit du Soleil. ]]
[[ Si on simplifie, sur les 44 TW thermiques évacués par la Terre, 2/3 le sont par les océans, et 1/3 par les continents. ]]
[[ Si on ajoute toutes les productions des sources d’énergies internes à la Terre (radioactivité, cristallisation de la graine, énergies gravitationnelle et des marées), on arrive à une puissance totale de 21+1+1+0,1 = 23±4 TW. Or la Terre dégage ≈46 TW. Une moitié de la puissance dégagée par la Terre n’est donc pas produite par une quelconque source d’énergie, mais par le refroidissement de la masse de la Terre, que l’on appelle refroidissement séculaire. ]]
Merci beaucoup pour vos intéressantes précisions sur les ordres de grandeurs.
La climatologie a longtemps été seulement descriptive, par les géographes et les historiens.
Depuis quelques décennies, des modélisateurs du climat, proposent des projections au-delà du siècle. Elles sont, pour l’instant, majoritairement démenties par les observations.
Il est permis de douter que nous puissions prévoir le climat dans un siècle.
Il est certain que 0.015 PW ou 0,046 PW sont quasi négligeables relativement à la puissance solaire en haute atmosphère ≈ 174 PW.
Mais ces 174 PW finirons par être rayonnés par la Terre, soit sous forme visible (albédo) de l’ordre de 54 PW, soit sous forme IR, de l’ordre de 120 PW.
Le volcanisme peut agir sur l’albédo, on ne peut donc conclure à un effet négligeable du volcanisme malgré la faible puissance en jeu.
La question à résoudre concerne surtout les éventuelles variations de long terme pour la puissance solaire, elles sont difficiles à estimer.
En effet, les mesures de la TSI par un même satellite ne couvrent que la durée d’un cycle de 11 ans.
On mesure dans un unique cycle de 11 ans une variation de la TSI de l’ordre de 0,2% .
Une variation de la TSI de ≈ 1% (sur plusieurs cycles) permettrait d’expliquer une variation de « température » de ≈ 1K
Mais nous ne connaissons pas vraiment la variation à long terme car le raccordement des mesures, avec un autre satellite, est sujet à discussion.
Voir ceci : https://climatedataguide.ucar.edu/sites/default/files/styles/node_lightbox_display/public/key_figures/climate_data_set/swsc130036-fig1.png?itok=aVmxYHWC
A propos de UAH : L’association des climato-réalistes organise lundi 6 mai à Paris une conférence avec le climatologue John Christy, professeur des sciences de l’atmosphère à l’Université d’Alabama à Huntsville qui vient d’être nommé conseiller scientifique de l’agence américaine de protection de l’environnement (EPA).
Depuis 1989, John Christy publie la « courbe UAH » de mesure satellitaire de la température de la Terre, ce qui lui a valu la prestigieuse médaille de la NASA pour réalisation scientifique exceptionnelle.
…………………………………………………………………………………………………………………………… Biography : https://www.uah.edu/science/departments/atmospheric-science/faculty-staff/dr-john-christy
Dr. John R. Christy is the Distinguished Professor of Atmospheric Science and Director of the Earth System Science Center at The University of Alabama in Huntsville where he began studying global climate issues in 1987. Since November 2000 he has been Alabama’s State Climatologist. In 1989 Dr. Roy W. Spencer (then a NASA/Marshall scientist and now a Principle Research Scientist at UAH) and Christy developed a global temperature data set from microwave data observed from satellites beginning in 1979. For this achievement, the Spencer-Christy team was awarded NASA’s Medal for Exceptional Scientific Achievement in 1991. In 1996, they were selected to receive a Special Award by the American Meteorological Society « for developing a global, precise record of earth’s temperature from operational polar-orbiting satellites, fundamentally advancing our ability to monitor climate. » In January 2002 Christy was inducted as a Fellow of the American Meteorological Society.