Samuel Furfari, Professeur à l’Université libre de Bruxelles,
et Henri Masson, Professeur (émérite) à l’Université d’Antwerpen
English (original) version here
La traduction a été assurée par Pierre Granperrin membre de l’Association des climato-réalistes (ici)
L’augmentation de la température au cours de la période 1980-2000 a suscité un vif intérêt pour la question du changement climatique. Mais en réalité, de quelle température parlons-nous et quelle est la fiabilité des données correspondantes?
1. Les erreurs de mesure
Pendant environ 250 ans les températures ont été enregistrées avec des thermomètres, puis depuis quelques décennies par des capteurs électroniques ou des satellites. Pour les données plus anciennes, on s’appuie sur des « proxies » (indicateurs tels que cernes d’arbres, stomates ou autres preuves géologiques nécessitant une calibration du temps et de l’amplitude, des chroniques historiques des almanachs, etc.). Chaque méthode comporte une erreur expérimentale, typiquement 0,1 ° C pour un thermomètre, beaucoup plus pour les « proxies ». Le passage d’une méthode à une autre (par exemple d’un thermomètre à un capteur électronique ou d’un capteur électronique à des données satellitaires) nécessite un calibrage et un ajustement des données qui ne sont pas toujours parfaitement documentés dans les enregistrements. En outre, comme indiqué plus loin dans cet article, la durée de la fenêtre de mesure est d’une importance capitale pour pouvoir tirer des conclusions sur l’existence éventuelle d’une tendance dans les données climatiques observées. Un certain compromis est requis entre l’exactitude des données et leur représentativité.
2. Erreurs de moyennes temporelles
Si l’on s’intéresse uniquement aux mesures « fiables » effectuées à l’aide de thermomètres, il est nécessaire de définir des températures journalières, hebdomadaires, mensuelles et annuelles moyennes. Mais avant l’utilisation des capteurs électroniques qui permettent un enregistrement quasi continu des données, ces mesures étaient effectuées ponctuellement, à la main, plusieurs fois par jour. L’algorithme de calcul de la moyenne quotidienne utilisé varie d’un pays à l’autre et dans le temps, d’une manière qui n’est pas parfaitement décrite dans les données, ce qui induit des erreurs (Limburg, 2014). De plus, la température suit des cycles saisonniers, liés à l’activité solaire et à l’exposition locale au soleil (angle d’incidence des rayonnements solaires), ce qui signifie qu’en comparant les données mensuelles, on compare les températures (du début à la fin du mois) correspondant à différents points du cycle saisonnier. Enfin, comme le sait tout jardinier amateur, les cycles de la Lune ont également un effet détectable sur la température (un cycle de 14 jours apparaît dans les données de température locales, correspondant à l’harmonique 2 du mois de la Lune, Frank, 2010); il y a environ 13 cycles lunaires de 28 jours sur une année solaire de 365 jours, mais l’année solaire est divisée en 12 mois, ce qui induit des biais et des tendances factices (Masson, 2018).
3. Les températures moyennes spatiales
Tout d’abord, le GIEC considère des températures globales moyennes du globe, malgré le fait que la température soit une variable intensive, une catégorie de variables n’ayant qu’une signification thermodynamique locale, et qu’il soit bien connu que la Terre présente des zones climatiques différentes qui sont bien documentées.
Les données utilisées proviennent des enregistrements des stations météo et sont supposées être représentatives d’une zone entourant chacune des stations météo formant l’ensemble de tous les points plus proches de cette station que de tout autre (algorithme de Voronoï). Comme les stations ne sont pas réparties de manière homogène et que leur nombre a considérablement évolué dans le temps, des « erreurs algorithmiques » sont associées à cette méthode de moyennage spatial. Egalement se reporter ici.
————————————————————————————————————————
DIAGRAMME DE VORONOI
«En mathématiques, un diagramme de Voronoï est une partition d’un plan en régions basées sur la distance par rapport à des points d’un sous-ensemble spécifique du plan. Cet ensemble de points (appelés stations, sites ou générateurs) est spécifié à l’avance, et pour chaque station, il existe une région correspondante constituée de tous les points plus proches de cette station que de toute autre. Ces régions sont appelées cellules de Voronoï.
[source: https://en.wikipedia.org/wiki/Voronoi_diagram]
À mesure que le nombre de points de départ change, les cellules correspondantes changent de forme, de taille et de nombre (figures 1 et 2).

Fig.1: Exemple de diagramme de Voronoï

Fig. 2: Idem avec un nombre réduit de localités (stations).
[construit avec http://alexbeutel.com/webgl/voronoi.html)
En climatologie, les points de départ sont les stations météorologiques et leur nombre a été considérablement réduit au fil du temps, ce qui modifie le nombre et la taille des cellules correspondantes (voir figures 3, 4 et 5).
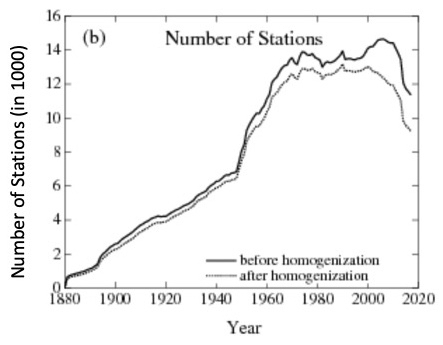
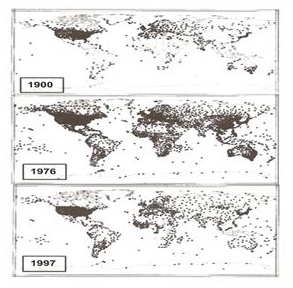
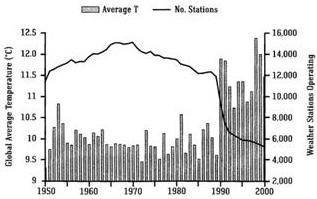
Fig. 5. Evolution des stations terrestres et de la température globale (Easterbrook 2016) [7]. Au début de 1990, des milliers de stations météorologiques situées dans des zones rurales plus froides (par exemple, en Sibérie, dans le nord du Canada) ont cessé d’enregistrer des données.
Nb : La figure 3 est basée sur GHCNv4 (de juin 2019) et la Figure 5 sur GHCNv2 (avant 2011). Toutes les stations ont été ré analysées ce qui explique les différences entre les deux figures.
Température moyenne
La température moyenne (en fait son anomalie, voir ci-dessous) est calculée en faisant la somme des données individuelles provenant des différentes stations et en attribuant à chaque point un poids proportionnel à la cellule correspondante (moyenne pondérée).
Comme la taille des cellules a changé au fil du temps, le poids des points d’origine (les stations météo) a également changé, ce qui induit un biais dans le calcul de la valeur moyenne globale.
————————————————————————————————————————
4. Effet d’ilot de chaleur urbain
En outre, de nombreuses stations météorologiques étaient initialement situées à la campagne, mais ces sites se sont progressivement urbanisés, causant un effet «d’îlot de chaleur urbain», qui augmente artificiellement la température mesurée (figures 6 et 7).
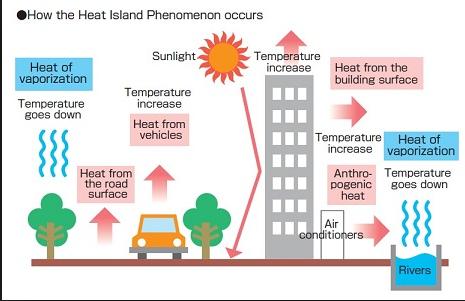
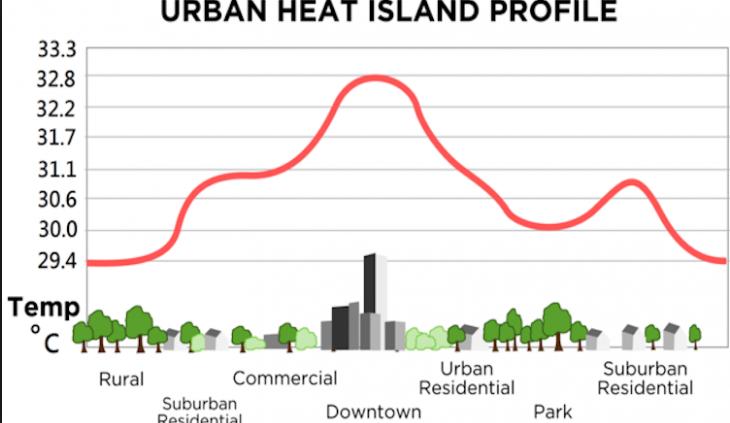
Fig. 6: Causes et illustration (Fig. 7) de l’effet d’îlot de chaleur urbain.
En conséquence, pour que les données des stations terrestres soient utiles, il est essentiel que tous les sauts de température non climatiques, tels que l’effet de l’îlot de chaleur urbain, soient éliminés. De tels sauts peuvent également être induits par le déplacement des stations ou la mise à jour de l’équipement. Dans la liste des données ajustées GISTEMPv4, l’effet de telles influences non climatiques est éliminé autant que possible. Initialement, seuls les cas documentés étaient ajustés. Cependant, la procédure actuelle utilisée par la NOAA / NCEI applique un système automatisé basé sur des comparaisons systématiques avec les stations voisines pour traiter les fluctuations documentées et non documentées qui ne sont pas directement liées au changement climatique. Les protocoles utilisés et l’évaluation de ces procédures sont décrits dans de nombreuses publications – par exemple [2, 3].
Cependant, corriger un effet d’ilot de chaleur urbain par homogénéisation avec des données venant de stations météo voisines, non urbanisées, pose problème. En effet, tout comme les données de la station « urbanisée » sont tempérées par les données des stations voisines non urbanisées, chacune de celle-ci voit ses données originales affectées par les données récoltées à la station urbanisée, et devient donc elle-même affectée (artificiellement) d’un effet d’ilot de chaleur urbain. Cette influence mutuelle réciproque, son effet pervers, et les conclusions fallacieuses qui en découlent , sont très bien expliqués, progressivement, dans la vidéo ci-jointe :
5. La température de surface des océans

Fig. 8: Mesures SST (température de surface de la mer) et non-représentativité
6. Les anomalies de température
Àun moment donné, la température sur Terre entre les points situés dans des régions polaires et ceux situés dans des régions équatoriales, peut varier de 100 °. Pour résoudre ce problème, le GIEC ne fait pas référence à la température absolue mais à ce que l’on appelle les « anomalies de température ». Pour cela, il calcule d’abord la température moyenne sur des périodes de référence fixes de 30 ans: 1931-1960, 1961-1990. La prochaine période sera 1991-2020. Ils comparent ensuite chaque température annuelle avec la température moyenne sur la période de référence la plus proche. Actuellement et jusqu’en 2021, l’anomalie est la différence entre la température actuelle et la moyenne sur la période 1961-1990.
Cette méthode repose sur l’hypothèse implicite que la température « naturelle » reste constante et que toute tendance détectée est causée par des activités anthropiques. Mais même dans ce cas, on s’attend à devoir procéder à certains ajustements, lors du passage d’une période de référence à l’autre, une tâche qui interfère avec la compensation d’un éventuel « îlot de chaleur urbain » ou avec une modification du nombre de stations météorologiques, deux effets que nous avons identifiés comme sources d’erreur et de biais.
Mais en réalité, le problème clé est que les enregistrements de température subissent localement des fluctuations polycycliques naturelles, fluctuations qui ne sont pas exactement périodiques et qui ne sont pas synchronisées [4]. Le fait que ces fluctuations ne soient pas exactement périodiques rend mathématiquement impossible la neutralisation d’ une tendance dans une série de données, en soustrayant une sinusoïde, comme cela est couramment fait, par exemple, pour corriger les variations saisonnières des données.
La durée de ces cycles est comprise entre un jour et une année, une décennie, un siècle, un millénaire et au-delà des dizaines de milliers d’années (cycles de Milankovich).
Les cycles décennaux présentent un intérêt particulier pour notre discussion car leur présence a une triple conséquence :
Premièrement, comme ils ne peuvent pas être correctement neutralisés car ils sont a-périodiques, ils interfèrent et amplifient un effet anthropique éventuel et s’intègrent aux anomalies.
Deuxièmement, ils induisent des biais et de fausses anomalies dans le calcul de la température moyenne sur la période de référence, comme le montre la figure ci-dessous (Masson, [5]).
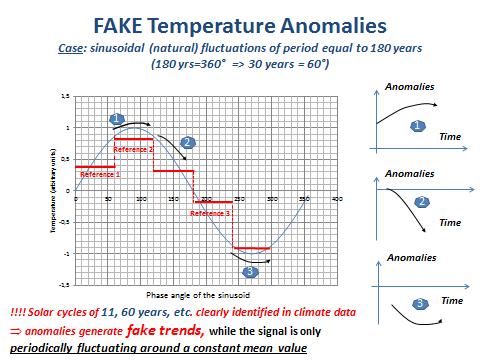
Fig. 9: Anomalies et signaux périodiques de période comparables à la longueur de la période de référence.
Commentaire sur la Fig. 9
La figure montre les problèmes associés à la définition d’une anomalie lorsque le signal comporte une composante périodique de longueur comparable à celle de la période de référence utilisée pour calculer cette anomalie. Pour simplifier, nous considérons une sinusoïde de période égale à 180 ans (une périodicité couramment détectée dans les signaux liés au climat), soit 360 ° = 180 ans et 60 ° = 30 ans (durée de la période de référence utilisée par le GIEC pour le calcul des anomalies). Pour notre propos, 3 périodes de référence de 60 ° (30 ans) ont été considérées le long de la sinusoïde (les lignes horizontales rouges signalées par les références 1, 2 et 3). Sur le côté droit du graphique, les anomalies correspondantes (mesures sur les 30 prochaines années moins la valeur moyenne sur la période de référence) ont été représentées. Il est évident que les anomalies présentent des tendances différentes. Évidemment aussi, toutes ces tendances sont fausses car le signal réel est une sinusoïde de valeur moyenne globale égale à zéro. En d’autres termes, il n’y a pas de tendance, seulement un comportement périodique.
La troisième critique fondamentale sur la manière dont le GIEC traite les données de température concerne son choix de s’appuyer exclusivement sur les droites de régression linéaire, bien que tout spécialiste des données sache qu’il faut envisager une fenêtre temporelle dépassant au moins 5 fois la période d’un cycle dans les données pour éviter les « effets de bord ». Pas de chance pour le GIEC, la plupart des données climatiques font apparaître des composantes cycliques significatives avec des périodes (approximatives) de 11, 60 et 180 ans, alors que par ailleurs le GIEC prend en compte une fenêtre temporelle de 30 ans pour le calcul des anomalies.
Ainsi, le GIEC crée une « accélération artificielle du réchauffement planétaire » en calculant les tendances linéaires à court terme à partir de données présentant une signature cyclique. Sur la figure 10 extraite de la FAQ 3.1 du chapitre 3 de son rapport AR4 de 2007 [6], le GIEC indique « notez que pour les périodes récentes les plus courtes, la pente est plus grande, indiquant un réchauffement accéléré ».
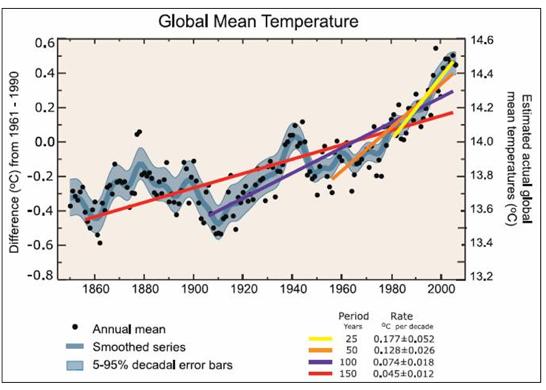
Fig. 10: Fausses conclusions du GIEC
Le graphique suivant (Fig. 11) illustre le problème.
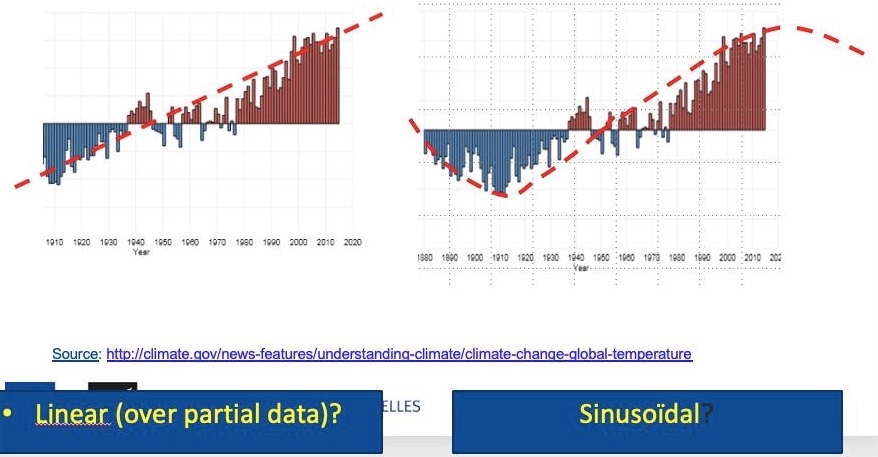
Fig. 11: Températures mondiales comparées à la température mondiale moyenne pour la période 1901-2000.
Commentaire sur la figure 11
Le graphique montre la température mondiale moyenne annuelle depuis 1880 comparée non pas à une période de référence de 30 ans (comme cela est fait pour le calcul des anomalies), mais à la moyenne à long terme de 1901 à 2000. Le zéro correspond à la moyenne à long terme de l’ensemble de la planète, les barres indiquent les « anomalies » globales (mais à long terme) supérieures ou inférieures à la moyenne à long terme par rapport au temps. La tendance linéaire revendiquée représentée sur la partie gauche de la figure n’est (plus que probablement), rien d’autre que la branche ascendante d’une sinusoïde de 180 ans comme le montre la partie droite de cette figure. C’est aussi une autre façon (la plus correcte et la plus simple?) d’expliquer l’existence de la « pause » ou du « hiatus » observé au cours des 20 dernières années. La « pause » correspondant au maximum de la sinusoïde et on pourrait s’attendre par conséquent à une période de refroidissement global au cours des prochaines années.
7. Tendances linéaires et données à signature cyclique
Enfin, les graphiques suivants (figures 12, 13 et 14 de Masson [5]) illustrent « l’effet de bord » mentionné précédemment pour un cas schématique et montrent les erreurs potentielles qui peuvent être commises lors de la manipulation avec des méthodes de régression linéaire de données ayant une composante cyclique avec une (pseudo) période de longueur comparable à la fenêtre temporelle considérée. La sinusoïde reste exactement la même (et ne montre aucune tendance), mais si on calcule la tendance par régression linéaire ( en appliquant la méthode des moindres carrés) sur une période de la sinusoïde, on obtient une FAUSSE droite de tendance dont la pente dépend de la phase initiale de la fenêtre temporelle considérée.
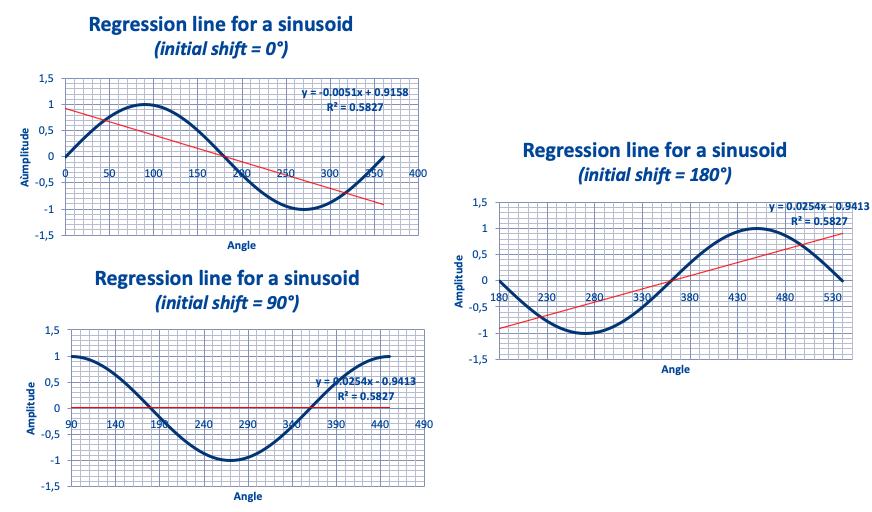
Figures 12, 13 et 14: ligne de régression linéaire sur une seule période d’une sinusoïde.
Lignes de régression pour une sinusoïde.
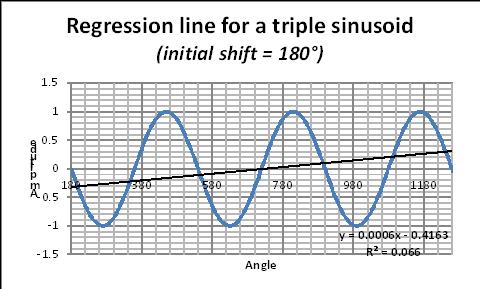
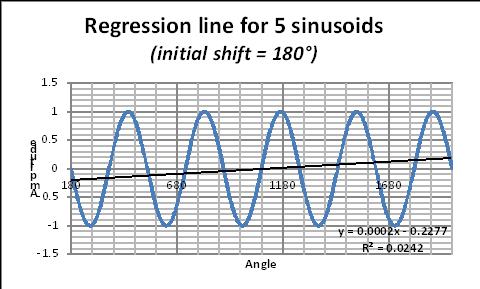
Pour illustrer le problème associé à «l’effet de bord» lors du tracé de la droite de régression d’une sinusoïde, considérons une simple sinusoïde et calculons la droite de régression sur un, deux, cinq,… de «nombreux » cycles (figures 15, 16, 17).
La sinusoïde étant stationnaire, la vraie droite de régression est horizontale (avec une pente = 0).
En prenant une phase initiale de 180 ° (pour générer une ligne de régression avec une pente positive), voyons comment la pente de la ligne de régression change avec le nombre de périodes :
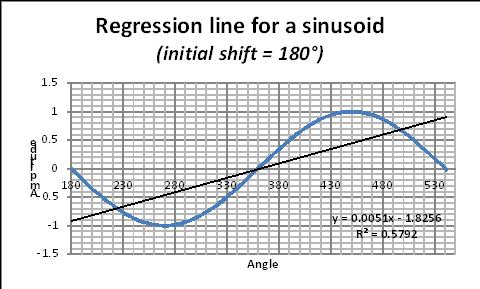
Figures 15, 16 et 17: Droite de régression pour des sinusoïdes à un, deux, cinq cycles.
L’équation de régression correspondante est donnée sur chaque figure. Dans cette équation, le coefficient de x donne la pente de la « fausse » droite de régression. La valeur de cette pente change avec le nombre de périodes comme cela est montré par la figure 18. En première approximation les spécialistes des données recommandent de prendre au moins six périodes.
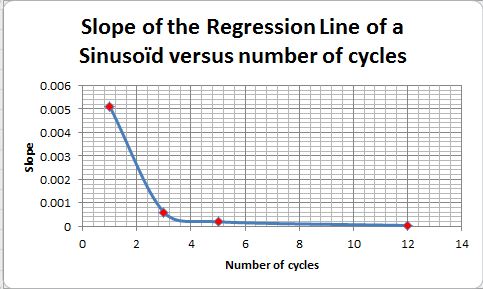
Fig. 18: Pente de la droite de régression en fonction du nombre de cycles (voir texte pour explication). Voir aussi le calcul sur tableur Excel / illustration (ici).
8. Un exemple utilisant des données réelles pour illustrer notre propos
Les considérations développées plus haut dans cet article paraitront probablement évidentes aux spécialistes expérimentés en traitement de données, mais il semble que la plupart des climatologues ne soient pas conscients (ou tentent de cacher ?) les problèmes associés à la durée de la fenêtre temporelle considérée et son moment initial. Comme dernière illustration, considérons les données climatiques «officielles »et voyons ce qui se passe lorsque l’on change la durée de la fenêtre de temps considérée et son instant initial (figures 19 à 21). Cet exemple montre de façon évidente que la méthode de régression linéaire appliquée à des données (poly)-cycliques de période similaire à la durée de la fenêtre temporelle considérée, ouvre la porte à toute sorte de fausses conclusions, voire à des manipulations visant à justifier tel ou tel programme politique.
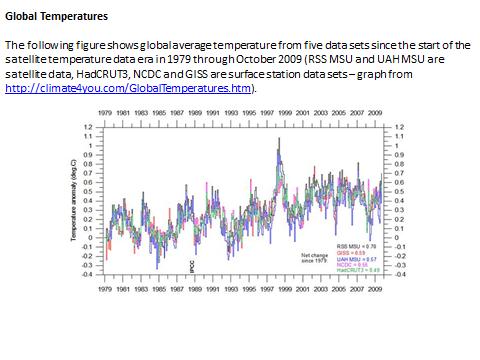
Fig. 19 : Un example des anomalies de températures globales ‘officielles ‘
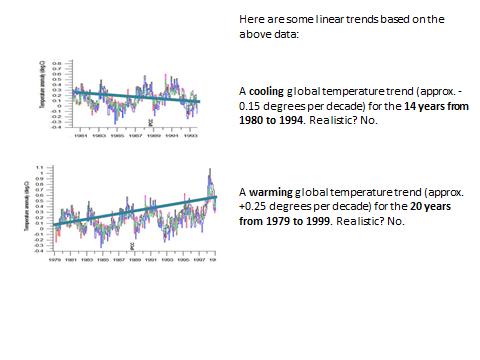 Fig. 20 : Effet de la durée, du temps initial et de la fenêtre temporelle
Fig. 20 : Effet de la durée, du temps initial et de la fenêtre temporelle
sur les droites de tendances linéaires
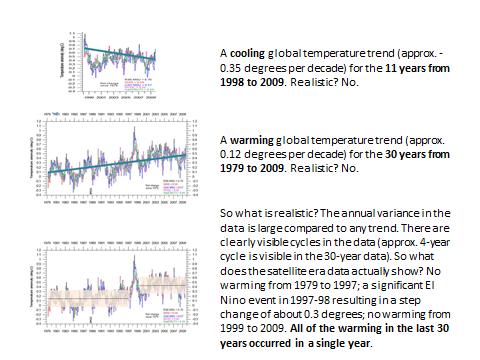
Fig. 21 : suite de figure 20.
Conclusions
- Les projections du GIEC résultent de modèles mathématiques qui doivent être calibrés à l’aide des données du passé. La précision des données utilisées pour le calibrage est d’une importance primordiale, car le système climatique est hautement non linéaire, tout comme les équations (Navier-Stokes) et les algorithmes (intégration de Runge-Kutta) utilisés dans les modèles informatiques du GIEC. Par conséquent, le système, ainsi que la façon dont le GIEC le représente, est extrêmement sensible aux changements infimes de la valeur des paramètres ou des conditions initiales (la calibration des données dans le cas présent), qui doivent être connus avec une grande précision. Ce n’est pas le cas, ce qui jette un doute sérieux sur toute conclusion que l’on pourrait tirer des projections de modèles.
- La plupart des données relatives au climat utilisées par le GIEC sont en vérité générées à partir de données météorologiques collectées dans des stations météorologiques terrestres. Cela a deux conséquences:
(i) La couverture spatiale des données est très discutable, car la température au-dessus des océans, qui représentent 70% de la surface de la Terre, est en grande partie négligée ou « déduite » par interpolation;
(ii) Le nombre et l’emplacement de ces stations météorologiques terrestres ont considérablement évolué au fil du temps, ce qui a entraîné des biais et de fausses tendances. - Le principal indicateur utilisé par le GIEC est l’anomalie de température globale, obtenue en faisant la moyenne spatiale des anomalies locales (autant que cela est possible). Les anomalies locales sont la comparaison de la température locale actuelle avec la température locale moyenne calculée sur une période de référence antérieure fixe de 30 ans, changeant toutes les 30 années (1930-1960, 1960-1990, etc.). Le concept d’anomalie locale est très discutable, en raison de la présence de composants polycycliques dans les données de température, induisant des biais considérables et de fausses tendances lorsque la « fenêtre de mesure » est plus courte que 6 fois la plus longue période détectable dans les données; ce qui est malheureusement le cas avec les données de température.
- Les méthodes de régression linéaire appliquées aux données (poly)-cycliques de période semblable à la fenêtre temporelle considérée, aboutissent à des conclusions erronées, voire à des manipulations destinées à soutenir des programmes politiques.
- Par conséquent, il serait souhaitable d’abandonner le concept d’anomalie de température globale et de nous concentrer sur des données météorologiques locales non biaisées afin de détecter un éventuel changement du climat local, qui est un concept physiquement significatif, et qui est après tout ce qui est réellement important pour les populations locales, l’agriculture, l’industrie, les services, les entreprises, la santé et le bien-être en général.
Notes
[1] The GISS Surface Temperature Analysis (GISTEMP v4) est une estimation du changement de la température de surface globale. Il est calculé à l’aide des fichiers de données provenant de NOAA GHCN v4 (stations météorologiques) et ERSST v5 (zones océaniques), combinés comme décrit dans Hansen et al. (2010) et Lenssen et al. (2019) (voir: https://data.giss.nasa.gov/gistemp/). En juin 2019, le nombre de stations terrestres était de 8781 dans l’ensemble de données non ajusté GHCNv4; en juin 1880, il n’y avait que 281 stations.
[2] Matthew J. Menne, Claude N. Williams Jr., Michael A. Palecki (2010) Sur la fiabilité du record de température de surface américain. JOURNAL DE RECHERCHE GÉOPHYSIQUE, VOL. 115, D11108, doi: 10.1029 / 2009JD013094, 2010.
[3] Venema VKC et al. (2012) Benchmarking homogenization algorithms for monthly data. Clim. Past, 8, 89-115, 2012.
[4] F.K. Ewert (FUSION 32, 2011, Nr. 3 p31)
[5] H. Masson, Complexity, Causality and Dynamics inside the Climate System (Proceedings of the 12thannual EIKE Conference, Munich November 2018)
[6] IPCC, http://www.ipcc.ch/pdf/assessment-report/ar4/wg1/ar4-wg1-chapter3.pdf]
[7] Easterbrook D.J. (2016) Evidence-based climate science. Data opposing CO2 emissions as the primary source of global warming. Second Edition. Elsevier, Amsterdam, 418 pp.