par Prof. Dr. Paul Berth
Selon un récent article du Guardian, des scientifiques ont mesuré pour la première fois la température de 20,75°C le 9 février 2020 sur l’île Seymour, une île située au large de la péninsule Antarctique. Cette île comporte la station de mesure Marambio où les relevés ont été réalisés. Bien entendu, cette nouvelle a été reprise par les médias, Greta Thunberg en tête. Cependant, en analysant objectivement la situation vous pourrez constater qu’il n’y a pas lieu de s’alarmer.
1. Localisation de l’île Seymour et température moyenne annuelle
L’île Seymour est située au large de la péninsule Antarctique (Figure 1), la région la plus au nord du continent Antarctique et, quasiment, la seule partie d’Antarctique s’étendant au-delà du cercle polaire.
L’article du Guardian nous donne le graphique de températures suivant pour le début du mois de février 2020 (Figure 2) :
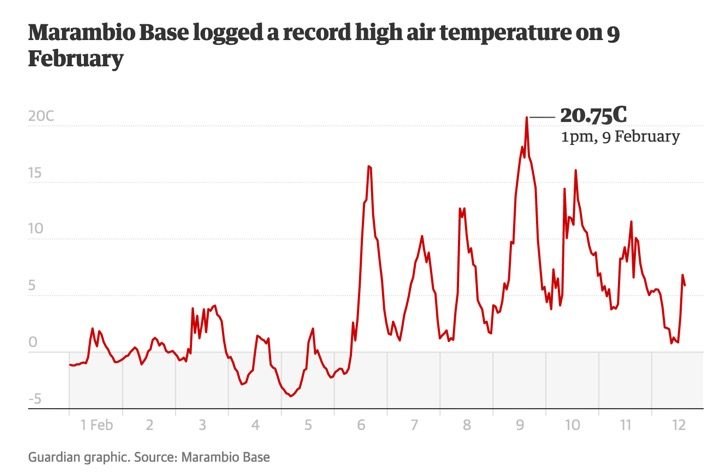
Nous pouvons voir en consultant l’axe des abscisses de la Figure 2 qu’il s’agit de températures journalières, relevées toutes les heures, avec des pics chaque jour aux heures les plus chaudes. Bien entendu il peut s’agir d’un record de température positive. Mais il ne faut jamais se fier à la température d’un seul jour. Une seule mesure ne veut rien dire, car il existe peut-être dans l’année des records de températures négatives au même endroit dont les médias ne parlent pas (les médias ne parlent jamais des records de basses températures, comme par exemple les –65°C en janvier 2020 au Groenland, voir ici). En moyenne, il se pourrait donc que la température ne varie pas.
Pour savoir ce qu’il en est, analysons les données officielles (Figure 3) de la station Marambio (données GHCNv4 fournies par la NOAA, ici) et regardons les températures moyennes annuelles. Les données ont été homogénéisées par la NOAA (c’est-à-dire nettoyées et corrigées des effets non climatiques).
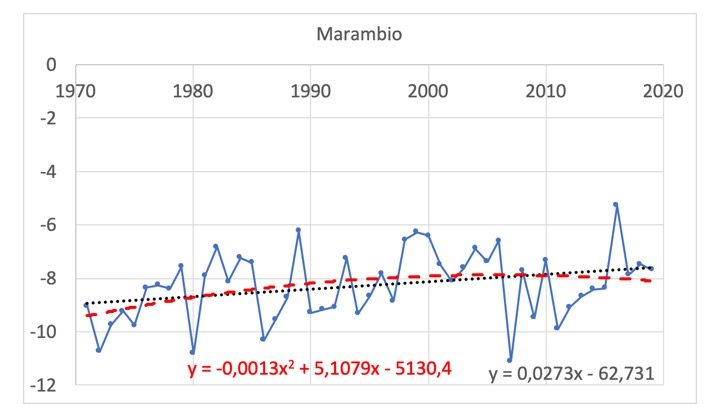
Nous constatons les choses suivantes :
– Depuis 1971, les valeurs de température moyenne annuelle de la station Marambio sont négatives, inférieures à –5°C. Les températures annuelles moyennes les plus récentes (2019) sont de –8°C. Ceci démontre que la zone reste assez froide.
– Il existe de grandes variations d’une année à l’autre, atteignant parfois + ou – 4,5°C en un an : par exemple de –6,60°C en 2006 on passe à –11,11°C en 2007.
– Si l’on trace une droite de régression, une très légère tendance positive est observée avec l’ensemble des données entre 1971 et 2019. La droite obtenue possède une faible pente de +0,027 (le coefficient de détermination R2 valant 0,09). Mais peut-on raisonnablement tracer une telle droite?
– Si au lieu de considérer une droite de régression on fait passer une polynomiale de degré 2 parmi les données on obtient un meilleur coefficient de détermination (R2 = 0,12). On constate alors (Figure 3) une légère augmentation de température entre 1970 et 1995, puis une température stable jusqu’en 2020. Depuis 1995, la température moyenne annuelle oscille autour de –8°C. Notons que dans la nature, les phénomènes sont rarement linéaires.
Concluons déjà pour la station Marambio : non, il n’y a pas d’augmentation folle de la température, particulièrement au cours des 25 dernières années.
2. Les autres stations de la péninsule Antarctique
Une seule station de mesure, comme celle de Marambio, ne suffit évidemment pas pour tirer des conclusions fiables. Voyons donc ce qu’il en est des stations proches (Figure 4).
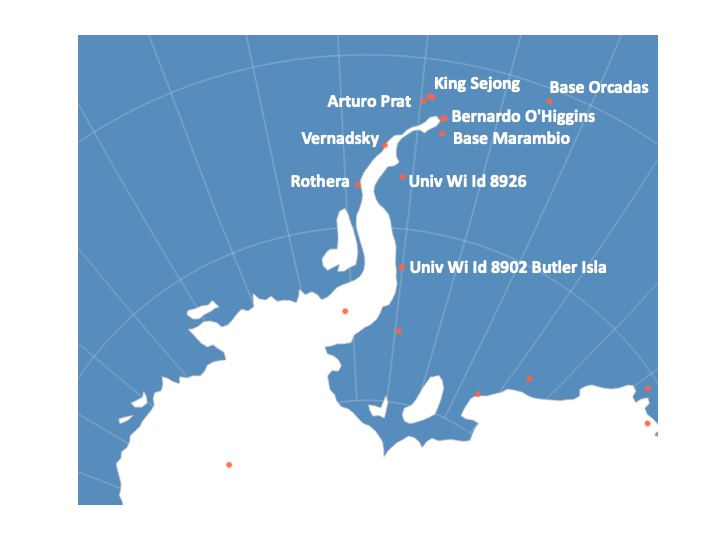
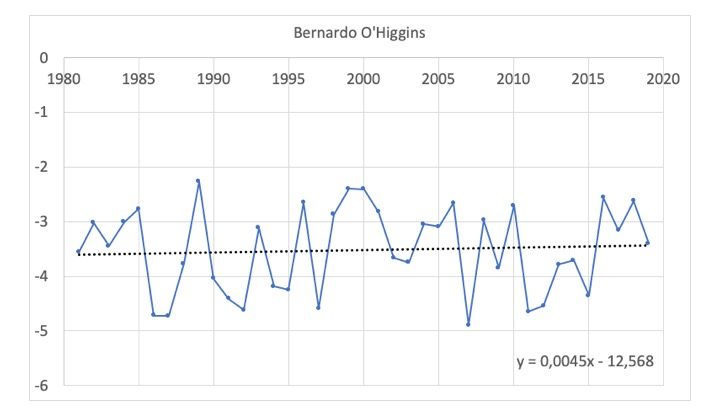
– Pour la station Bernardo O’Higgins, très proche de Marambio, les températures moyennes annuelles sont négatives avec une tendance stable depuis 1980 (Figure 5).
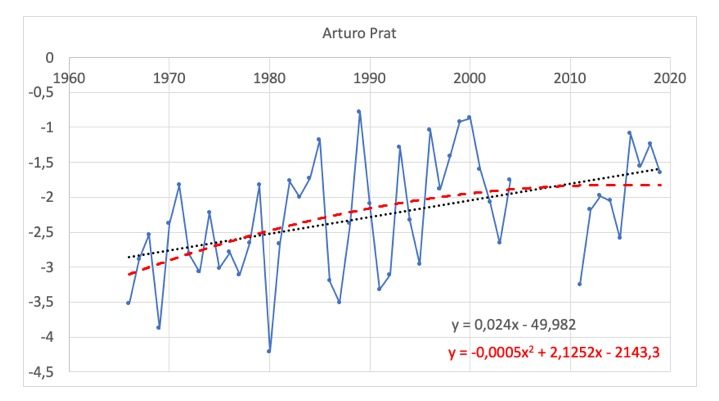
– Pour la station Arturo Prat (Figure 6) les températures moyennes annuelles sont également négatives. Encore une fois, on constate de grandes variations d’une année à l’autre, une légère pente de +0,02 si l’on trace une droite de régression avec l’ensemble des données (R2 = 0,20), mais une stabilisation de la température depuis 2000 si l’on trace une polynomiale (R2 = 0,22).
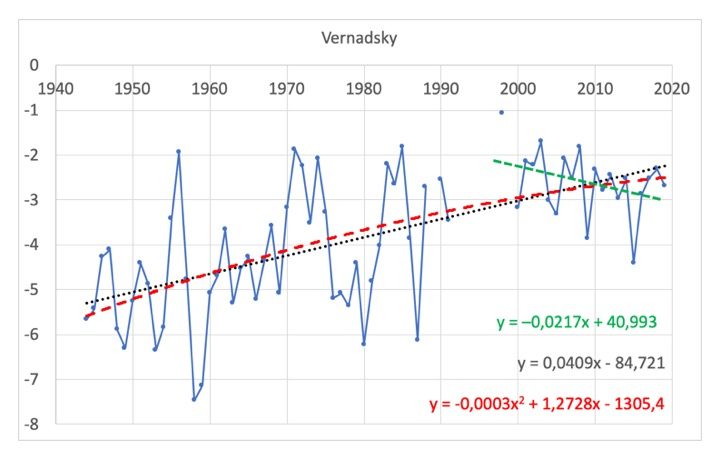
– Pour la station Vernadsky (Figure 7) nous constatons une tendance nettement décroissante en ne considérant les données que depuis l’année 2000 (pente de –0,021; droite verte sur Fig.7). Avec l’ensemble des données nous obtenons une droite de régression dont la pente est positive (valant +0,04; R2 = 0,3904). La polynomiale de degré 2 avec toutes les données donne encore une fois un R2 supérieur (0,3988). Ceci montre que si l’on considère toutes les données la température moyenne est en cours de stabilisation.
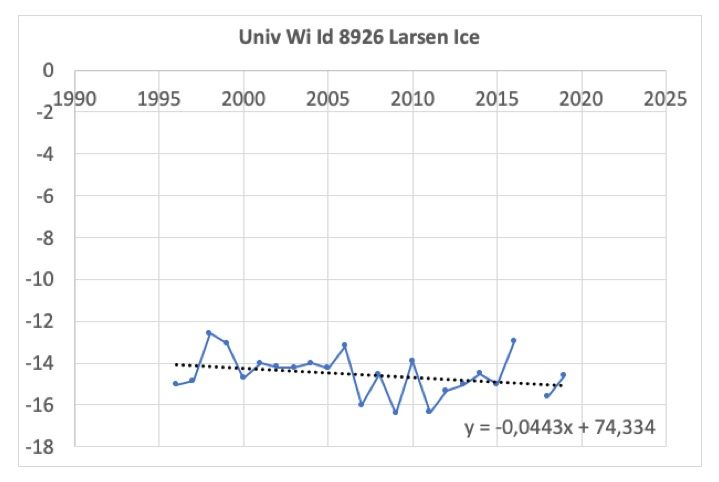
– Pour la station Univ Wi Id 8926 Larsen Ice (Figure 8), on constate aucune tendance à l’accroissement mais une diminution depuis 1995.
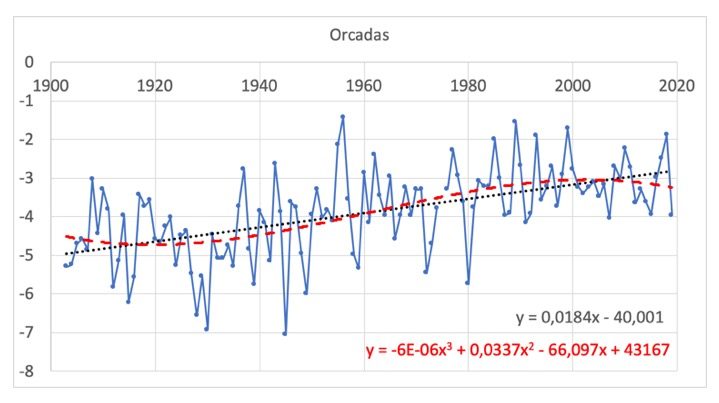
– Concernant la station Orcadas au large de la péninsule Antarctique (Figure 9) une décroissance est observée depuis 2000 avec cette fois-ci une polynomiale de degré 3 (R2 = 0,33). Comme à chaque fois, une droite avec l’ensemble des données depuis 1902 montre une légère tendance positive (pente de +0,01) mais le R2 est plus petit (0,30). Il vaut donc mieux considérer la courbe polynomiale.
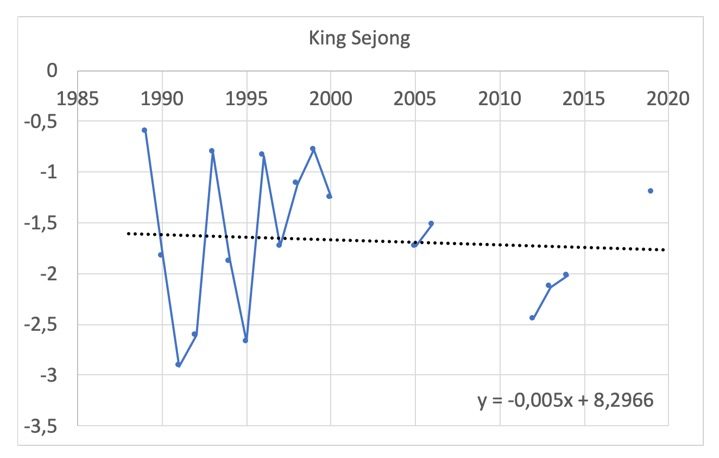
– Pour la station King Sejong (Figure 10) nous pouvons voir une diminution de la température moyenne annuelle depuis 1990, mais de nombreuses mesures sont manquantes.
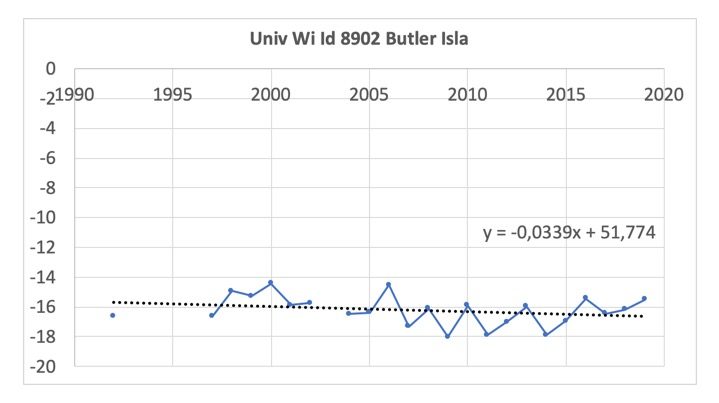
Finalement, pour la station Univ Wi Id 8902 Butler Isla (Figure 11) nous pouvons voir une diminution depuis 1997. Remarquons qu’en moyenne annuelle la température est ici inférieure à –14°C.
3. Conclusions
– Pour comprendre ce qu’il se passe dans un jeu de données de température il ne faut pas considérer une seule mesure comme le fait l’article du Guardian; il ne faut pas non plus considérer une seule station de mesure.
– Si l’on désire faire passer des droites parmi les données de température, les plus longues séries disponibles sont celles de la station Orcadas (depuis 1902), qui est quand même assez éloignée de la péninsule Antarctique. On constate alors un réchauffement d’environ + 2°C en 110 ans (la courbe de tendance coupe –5°C en 1900 et –3°C en 2010). Cependant, en considérant des courbes polynomiales dont le coefficient de détermination est meilleur on constate que les températures moyennes chutent depuis les années 2000, comme dans toutes les stations de la péninsule Antarctique présentées dans cet article.
– Les phénomènes naturels suivent rarement des droites. Ils sont généralement cycliques, avec des périodes et amplitudes très variables. Il est donc permis de conclure que la péninsule Antarctique ne se réchauffe pas depuis 25 ans. Ceci est confirmé par d’autres analyses (voir ici et ici) et il est dommage qu’une fois de plus les médias ne fassent pas plus preuve de rigueur et se permettent des raccourcis donnant une information inexacte à 100%. En sont-ils seulement conscients ?
Nous avions compris que les MSM nous ne racontent que a moitié de la vérité (le côté réchauffant). Nous comprenons maintenant qu’il ne s’agit que d’un quart de la vérité et j’estime qu’il s’agit d’une estimation très indulgente
Bonjour,
Merci pour ces infos.
Et en ce qui concerne l’étendue de la glace en antarctique, quelles sont les données ?
Cordialement
Bonjour. Pour des données actualisées sur l’étendue de la glace Antarctique vous pouvez consulter ce site : http://nsidc.org/arcticseaicenews/antarctic-daily-image-update/
Je suis d’accord sur le fond (pas de changement de température extraordinaire en Antarctique), mais pas sur l’argument des régressions quadratiques ou cubiques versus affines. Ces dernières ayant plus de paramètres, leur R2 ne peut qu’être plus grand que celui de la droite, mais cette supériorité n’est pas forcément significative. On peut soit la tester directement (ce que je ne peux pas faire sans les valeurs), soit corriger les R2 pour tenir compte du nombre différent de paramètres des modèles, ce que l’on appelle le R2 ajusté :
R2ajuste = R2 – (m-1)*(1-R2)/(n-m)
où n est le nombre de points, et m est le nombre de paramètres du modèle (m=2 pour la droite, et m=3 pour la parabole, m=4 pour le degré 3). Pour les figures 3, 6, 7 et 9, vous donnez :
R2droite= 0.09, 0.20, 0.3904, 0.30
R2parabole = 0.12, 0.22, 0.3988, 0.33
En prenant n = 49, 48, 67, 116 respectivement (d’après les figures), on obtient :
R2ajudroite = 0.0706 0.1826 0.3810 0.2939
R2ajuparabole = 0.0817 0.1853 0.3800 0.3121
En tenant compte des nombres de degrés de liberté, la droite affine est donc suffisante pour le troisième cas, et dans les trois autres, la supériorité du modèle de degré supérieur n’est pas écrasante.
@ Ravilo
Je suis parfaitement d’accord avec vous. Un grand merci pour ces précisions!