La formule de Stefan-Boltzmann est l’outil de travail des climatologues qui veulent prédire des variations de température à partir des flux énergétiques intervenant dans le bilan énergétique de la Terre ( voir ici ). Sous la forme utilisée, elle lie le flux unidirectionnel F rayonné (vers la Terre ou vers l’espace) à la température T (en K) à la puissance 4 (σ = constante de Stefan = 5,67 x 10-8 W m-2 K-4) :
F (W m-2) = σ T4 (1)
Rappel théorique
La formule de Stefan-Boltzmann est dérivée de la théorie du « corps noir » élaborée par plusieurs physiciens dans la seconde moitié du 19ème siècle pour établir un lien entre le flux de rayonnement émis par tout solide à une température supérieure au zéro absolu et la température de ce solide. La meilleure représentation qu’on puisse se faire du modèle sur lequel est basée cette théorie est celle d’un four sous vide et à l’équilibre thermique dont la paroi interne opaque absorbe, sans aucune réflexion ni transmission, tout rayonnement électromagnétique quelle que soit sa longueur d’onde. A l’équilibre thermique elle doit également réémettre tout rayonnement absorbé. Ce four parfaitement isolé devrait cependant être percé d’un minuscule orifice permettant d’analyser le rayonnement concentré à l’intérieur. Aucune interprétation quantitative du spectre observé ne fut possible dans le cadre de la théorie électromagnétique classique et c’est finalement Planck qui proposa en 1900 une équation introduisant l’idée, révolutionnaire pour l’époque, qu’à chaque longueur d’onde le rayonnement ne peut être émis que sous forme de « quanta » (c’est-à-dire de petits paquets) dont l’énergie est hν = hc/λ (où ν et λ sont respectivement la fréquence et la longueur d’onde du rayonnement, c la vitesse de la lumière et h une nouvelle constante de la nature appelée désormais constante de Planck). Ce rayonnement qualifié de « thermique » est dû à l’oscillation de dipôles électriques formés par le noyau et le nuage électronique des atomes qui, en accord avec les lois de l’électromagnétisme, émettent un rayonnement de fréquence égale à la fréquence d’oscillation.
L’équation de Planck (mentionnée sur la fig. 1) permet de calculer à différentes températures l’émittance monochromatique hémisphérique E(λ, T) en W m-2 c’est-à-dire le flux par unité de surface émis à chaque longueur d’onde dans toutes les directions à partir d’une surface plane. Les courbes obtenues sont présentées sur la fig. 1. Elles sont indépendantes de la nature du corps.
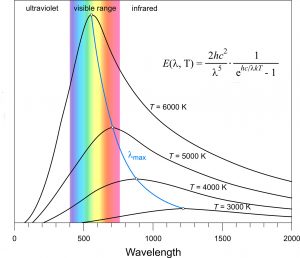
Fig. 1 Equation de Planck donnant E (λ, T) en fonction de la longueur d’onde (en nm)
L’intégration de l’équation de Planck sur tout le domaine de longueurs d’onde conduit à la formule de Stefan-Boltzmann qui lie l’émittance hémisphérique totale E(T) (en W m-2) à la température T (en K) à la puissance 4 (σ = constante de Stefan) :
E (T)(W m-2) = σ T4 (2)
La relation (2) fournit une mesure de l’aire sous les courbes de la fig. 1. Il faut remarquer que l’émittance énergétique hémisphérique E(T) intervenant dans la relation (2) est physiquement différente du flux unidirectionnel F de la relation (1). Cette dernière, couramment utilisée en climatologie, peut être considérée comme une approximation à usage pratique. La fig. 1 montre aussi que le maximum de la courbe d’émission se déplace avec la température selon la loi de Wien :
λmax = C / T (C = 2,9 10-3 m K).
Limitations pratiques
L’application de l’équation de Planck et de la formule de Stefan-Boltzmann à des substances réelles bien différentes du modèle théorique implique certaines limitations.
1° En présence d’un autre corps à une température supérieure au zéro absolu, émettant donc aussi un rayonnement thermique, l’échange énergétique radiatif obéira à la relation :
F (W m-2) = σ (Tc4 – Tf4)
Dans cette formule Tc et Tf sont respectivement les températures des corps chaud et froid impliqués dans l’échange énergétique (le symbole F correspond toujours à un flux unidirectionnel comme il est d’usage en climatologie). Le rayonnement émis par un corps froid ne peut donc pas être absorbé par un corps chaud. A titre d’exemple, on remarque sur la fig. 1 que toutes les longueurs d’onde émises par un corps à 3000 K sont déjà émises par un corps à 4000 K. Elles ne pourront donc être absorbées pour exciter l’oscillation de nouveaux dipôles dans ce corps plus chaud.
2° En toute rigueur l’équation de Planck et la formule de Stefan-Boltzmann ne peuvent être utilisées que si le rayonnement thermique est le seul mécanisme d’échange énergétique. Elle ne peut donc s’appliquer à la Terre où la convection de l’air et l’évaporation de l’eau des océans contribuent de manière prépondérante au bilan énergétique ( voir la fig. 1 ici ). Si les satellites détectent au sommet de l’atmosphère l’émission sous forme de rayonnement de 240 W m-2 on ne peut en déduire, par application de la formule (1), que la surface terrestre devrait être à la température de 255 K (-18°C). De même, le fait que la température « globale moyenne » de la Terre soit 288 K (15°C) ne permet pas d’en déduire que le flux radiatif émis par la Terre serait de 390 W m-2
3° Dans la pratique, la surface d’un corps réel ne se comporte pas comme celle d’un corps noir notamment car une partie du flux incident est réfléchie. On définit alors l’émissivité ε d’un corps quelconque comme le rapport entre le flux d’énergie radiative émis par ce corps et le flux d’énergie radiative qui serait émis par un corps noir à la même température. Pour un corps noir ε = 1 et pour un corps réel ε < 1. On qualifie ces corps de « gris » si l’équilibre thermique est néanmoins maintenu à toutes les longueurs d’onde ce qui implique que le flux émis reste égal au flux absorbé. L’absorptivité α d’un corps « gris » (définie de manière analogue à son émissivité) doit donc toujours être égale à son émissivité : α = ε (loi du rayonnement de Kirchhoff). Si α ≠ ε le corps n’est ni gris, ni noir et est hors d’équilibre thermique. Dans le cas d’un corps « gris » la formule de Stefan-Boltzmann devrait s’écrire :
F (W m-2) = ε σ T4 (3)
A une même température le flux radiatif émis par un corps gris sera moindre que celui émis par un corps noir. Les courbes de Planck seront semblables à celles de la fig. 1 mais les intensités émises seront plus faibles.
4° D’une manière générale, lorsque la surface d’un corps est soumise à un rayonnement incident, une fraction ρ (réflectivité) de l’énergie incidente est réfléchie, une fraction α (absorptivité) est absorbée et une fraction τ (transmissivité) est transmise (fig. 2). L’importance de ces différentes fractions dépend de la longueur d’onde et de la température mais la conservation de l’énergie implique toujours que : ρ + α + τ = 1. Dans le cas d’un corps noir ou gris τ = 0 d’où α = 1 – ρ. De plus, α = ε d’après la loi du rayonnement de Kirchhoff. Dans l’un et l’autre cas la formule de Stefan -Boltzmann peut être utilisée sous la forme (1) ou (3) mais elle n’est pas valable si τ ≠ 0.
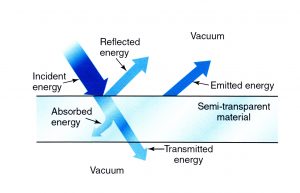 Fig. 2 Interactions d’un rayonnement incident avec une surface
Fig. 2 Interactions d’un rayonnement incident avec une surface
Dans le bilan énergétique de la Terre proposé par la NASA (voir la fig.1 ici) 4 % du flux radiatif d’origine solaire sont réfléchis par la surface terrestre (ρ = 0,04). L’absorptivité moyenne de la Terre serait donc α = 0,96. La Terre pourrait être considérée comme un corps gris si ce n’est que 71 % de sa surface sont occupés par des mers ou des océans. Or, l’eau est pratiquement transparente dans le domaine le plus intense du rayonnement solaire (400 nm à 1 µm) où son coefficient d’absorption est très faible (fig. 3). Comme τ ≠ 0 dans ce domaine de longueurs d’onde elle ne peut être considérée comme un corps gris et la formule de Stefan-Boltzmann n’est pas applicable.
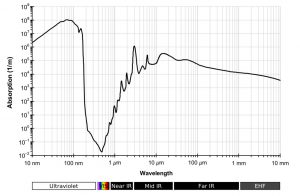
Fig. 3 Spectre d’absorption de l’eau
Néanmoins, pour estimer la température de surface des océans, des mesures du rayonnement émis ont été faites par satellite dans la fenêtre de transparence atmosphérique de 8 à 13 µm (voir la fig. 2 ici ) où le coefficient d’absorption de l’eau est beaucoup plus élevé (fig. 3). Dans cet intervalle de longueurs d’onde la pénétration du rayonnement solaire est limitée à quelques µm de la surface et τ = 0. La formule de Stefan-Boltzmann a alors été utilisée pour déterminer la température de surface de la mer et des océans dans différentes régions du globe. Il ne faut cependant pas oublier (voir rappel théorique) que la formule de Stefan-Boltzmann est obtenue par intégration de l’équation de Planck sur tout le domaine de longueurs d’onde rayonné et que relation en T à la puissance 4 n’est valable que dans ces conditions. L’application à la mesure de la température de surface des océans dans un domaine très limité de longueurs d’onde constitue donc une approximation.
5° Les basses couches atmosphériques ne peuvent jouer le rôle de corps noir car elles n’en présentent aucune des caractéristiques spécifiques. Elles n’ont pas de surface, les transferts énergétiques n’y sont pas exclusivement radiatifs et elles n’absorbent ni émettent toutes les longueurs d’onde puisque les constituants atmosphériques présentent un spectre de raies en absorption comme en émission.
Merci pour cet excellent article. La formule de Stefan-Boltzmann est malheureusement employée par les climatologues…et le premier à l’avoir employée est le chimiste et prix Nobel Svante Arrhenius!
merci pour cet article .
pour expliquer l’effet de serre ,lié a l’augmentation de CO2 l’altitude d’émission IR dans l’espace est plus haute donc la t° est plus basse.
Pour calculer la différence de puissance IR émise entre deux altitudes d’émission , que doit t-on utiliser ?
Votre question est basée sur l’hypothèse que l’effet de serre existe dans les bases couches atmosphériques. Je ne peux y répondre car je ne partage pas cette opinion (voir http://www.science-climat-energie.be/2019/02/14/le-rechauffement-climatique-dorigine-anthropique/ Pour alimenter le débat, si mes arguments ne sont pas convaincants, vous pourrez éventuellement trouver une réponse à votre question sur un site qui défend une opinion différente de la mienne : https://climatorealiste.com/effet-de-serre/ .
merci beaucoup, les tenants de cette hypothèse utilisent la formule de SB , ce qui ne me semble pas correct.
Bonjour,
Permettez-moi d’apporter quelques commentaires sur les section 1° et 2° :
1° La formule F = sigma (T1^4 – T2^4) permet de calculer le transfert NET d’énergie, elle ne représente donc pas un flux unidirectionnel de T1 vers T2, c’est un bilan des flux. Le corps T1 rayonne vers T2 un flux égale à sigma x T1^4, et le corps T2 rayonne vers T1 un flux égal à T2^4. Il n’y a là aucune violation de la thermodynamique étant donné que le transfert NET est positif du plus chaud (T1) vers le plus froid (T2).
Vous affirmez : « Le rayonnement émis par un corps froid ne peut donc pas être absorbé par un corps chaud. » C’est faux, et heureusement ! Si cela était vrai, alors des tas d’équipements ne pourraient pas fonctionner : fours à micro-ondes, récepteurs radio, radio-téléscopes,… On ne pourrait même pas mesurer la température du fond diffus cosmologique, de lo’rdre de 3K ! Même si on met de côté cette objection empirique, comment voulez-vous qu’un photon émis par la source froide ne puisse pas être absorbé par la source chaude ?
2° Vous dites : « En toute rigueur l’équation de Planck et la formule de Stefan-Boltzmann ne peuvent être utilisées que si le rayonnement thermique est le seul mécanisme d’échange énergétique. Elle ne peut donc s’appliquer à la Terre où la convection de l’air et l’évaporation de l’eau des océans contribuent de manière prépondérante au bilan énergétique. »
C’est faux à plus d’un titre. D’abord, la convection et l’évaporation ne contribuent pas au bilan radiatif de la Terre. Il s’agit de mécanismes de conversion de l’énergie thermique en énergie potentielle gravitationnelle, et cette énergie ne sort donc pas de la troposphère, la convection et l’évaporation s’arrêtant par définition au sommet de la troposphère. Ensuite, la convection et l’évaporation se passent à des vitesses bien inférieures (~500m/s) que le transfert radiatif (~vitesse de la lumière). Dès lors, du point de vue du rayonnement, et donc de la loi de Planck et ses corollaires, la convection et l’évaporation ne changent rien. Enfin, le gradient thermique adiabatique, qui est maintenu par le mécanisme de convection, n’empêche pas la troposphère d’être en équilibre thermodynamique local (LTE en anglais), qui est la seule condition requise pour qu’on puisse impunément appliquer la loi de Planck. (Je vous renvoie aux travaux de Milne en 1928, qui a soigneusement étudié l’effet des collisions moléculaires sur la condition d’équilibre thermodynamique local.)
Votre commentaire révèle une lecture un peu superficielle du texte cité. Si vous le relisez plus attentivement vous remarquerez que :
1° la phrase “Le rayonnement émis par un corps froid ne peut donc pas être absorbé par un corps chaud.” s’applique à un « corps noir » qui, à l’équilibre thermique, ne peut absorber plus qu’il n’émet et réciproquement. La phrase ne s’applique PAS à n’importe quelle source de rayonnement. De plus, il n’est nullement question de « violation de la thermodynamique » comme vous le prétendez.
2° la notion de « flux unidirectionnel » rayonné vers la Terre ou vers l’espace est une approximation utilisée spécifiquement par les climatologues. La formule de Stefan-Boltzmann envisage l’« émittance hémisphérique totale » seule notion ayant un sens physique précis.
3° la phrase « la formule de Stefan-Boltzmann … ne peut s’appliquer à la Terre où la convection de l’air et l’évaporation de l’eau des océans contribuent de manière prépondérante au bilan ENERGETIQUE » ne fait pas allusion au bilan RADIATIF de la Terre comme vous l’avez compris. L’exemple cité devrait vous permettre de mieux comprendre le sens de la phrase : « Si les satellites détectent au sommet de l’atmosphère l’émission sous forme de rayonnement de 240 W m-2 on ne peut en déduire, par application de la formule de Stefan-Boltzmann que la surface terrestre devrait être à la température de 255 K (-18°C). De même, le fait que la température « globale moyenne » de la Terre soit 288 K (15°C) ne permet pas d’en déduire que le flux radiatif émis par la Terre serait de 390 W m-2 »
4° le reste de votre commentaire concernant notamment « la conversion de l’énergie thermique en énergie potentielle gravitationnelle » et « le gradient thermique adiabatique » est hors de propos car non discuté dans l’article cité.
Bonjour professeur,
Tout d’abord merci infiniment pour vos explications qui m’ont complètement convaincu. J’ai toutefois un petit problème avec le rayonnement émis par le sol quand je dois l’expliquer à des amis. Je comprends bien qu’on ne peut utiliser la loi de Stefan-Boltzmann car on ne peut l’appliquer que si les transferts sont exclusivement radiatifs. Cependant, cela n’est pas assez convaincant à leurs yeux. On me rétorque que lorsqu’on regarde le spectre d’absorption atmosphérique mesuré par satellite, on mesure bien un rayonnement de 240 W/m2 englobé sous une courbe de Planck d’un corps noir dont la surface est de 390 W/m2. J’ai dès lors pris un spectre et j’ai calculé le rayonnement reçu (par découpage en petites surfaces) et comparé avec la surface de la courbe englobante et je suis retombé sur un rapport identique de 240/390. Si le rayonnement IR de 240 W/m2 vient du sol (20 W/m2) et de l’atmosphère (220 W/m2), d’où viennent les 390 W/m2? Je réponds que ces 390 W/m2 n’existent pas et que les seuls rayonnements sont ceux absorbés et émis par le sol (174 W/m2) et absorbés et émis par l’atmosphère en raison du rayonnement solaire (66 W/m2). Ai-je raison ou dois-je aller chercher une explication dans le lapse rate pour trouver le rayonnement qui manquerait pour atteindre 390 W/m2? Auriez-vous un argument qui puisse convaincre mes amis car pour eux, le sol à 15°C émet obligatoirement des rayonnements comme un corps gris (0,95) soit environ 390 W/m2 et comme le soleil n’amène que 174 W/m2, il faut bien un apport d’énergie très conséquent pour permettre au sol d’être à 15°C.
Je suis un peu démuni devant leur argumentation et aimerais bien réussir à supprimer les fameuses back radiation de leur schéma!
Merci par avance de me consacrer un peu de temps en ces lendemains de fête. Tous mes voeux.
Merci pour votre commentaire et pour vos voeux. Au paragraphe 2 de ma note http://www.science-climat-energie.be/2019/02/14/le-rechauffement-climatique-dorigine-anthropique/ j’explique qu’une petite fraction seulement du rayonnement détecté par satellite provient directement de la surface terrestre car émise dans la zone de transparence atmosphérique entre 8 à 13 µm (env. 20 W m-2). Quel que soit le mécanisme de dissipation de l’énergie au niveau de la surface terrestre, en altitude toute cette énergie doit être convertie en rayonnement car c’est le seul mécanisme permettant de l’évacuer hors du système terrestre. En accord avec le bilan énergétique proposé par la NASA (fig. 2 de la note) les satellites détectent effectivement à des altitudes de l’ordre de 800 km un rayonnement moyen de 240 W m-2 qui provient essentiellement des couches supérieures de l’atmosphère à des températures beaucoup plus basses que celle de la surface terrestre. Les résultats des mesures par satellites sont présentés sous forme de courbes qui résultent d’un traitement informatique. Vous en trouverez des exemples sur le site http://climatemodels.uchicago.edu/models.html . Ces courbes « expérimentales » présentées en traits pleins sont, en général, comparées à des courbes en traits pointillés correspondant à des corps noirs à la température indiquée. Pour un vrai corps noir à 15°C on obtient bien 390 W m-2 alors que la valeur expérimentale pour la Terre est 240 W m-2. Je suppose que c’est l’explication à la divergence que vous mentionnez dans votre commentaire.
Merci beaucoup pour votre réponse et le fait que la majeure partie du rayonnement détecté par un satellite soit en fait émis par des zones plus froides (c’est-à-dire en altitude) est convaincante. En effet, ce rayonnement sera par conséquent moins énergétique que s’il était émis du sol.
Je me suis prêté à un petit calcul à partir d’un spectre d’absorption atmosphérique comparé à des courbes de corps noir. Voici le spectre que j’ai utilisé:
https://planet-terre.ens-lyon.fr/planetterre/objets/Images/bilan-radiatif-terre2/bilan-radiatif-terre2-fig13.gif
Après agrandissement, je l’ai quadrillé pour déterminer la surface sous la courbe qui doit correspondre à un rayonnement de 240 W/m2. Ce faisant, j’ai pu obtenir l’angle solide avec lequel ce spectre a été mesuré. Je l’estime compris entre 4,7 et 5 stéradians. La courbe englobante est celle d’une courbe de Planck pour un corps à environ 288 K et sa surface correspond assez bien à un rayonnement de 390 W/m2. Jusque là tout va bien!
Je me suis ensuite intéressé à la fenêtre atmosphérique allant de 8 à 13 microns et j’ai calculé la surface sous la courbe (la raie due à l’ozone incluse car je crois que son absorption se fait dans la stratosphère). Mon résultat m’a complètement stupéfait car j’obtiens une valeur proche de 200 W/m2 alors que je pensais comme vous et la NASA que le rayonnement provenant du sol était de 20 W/m2.
Je ne pense pas avoir fait d’erreur de mesures (même si elles ne sont pas d’une précision diabolique) mais il y a probablement quelque chose qui m’échappe dans la construction de ce spectre d’absorption. Auriez-vous l’amabilité d’éclairer ma lanterne, parce que s’il y a effectivement 200 W/m2, ça changerait bien des choses dans le bilan radiatif de la Terre! Merci d’avance.
D’abord, il faut remarquer que l’émission détectée par satellite entre 8 et 13 µm ne provient pas exclusivement de la surface terrestre mais aussi de différentes couches atmosphériques. Ensuite, la présentation du spectre auquel vous vous référez est inhabituelle car l’échelle des abscisses est en longueurs d’onde plutôt qu’en nombres d’onde (proportionnels à l’énergie). Le spectre est donc déformé et l’intégration graphique pour obtenir la puissance rayonnée n’est pas correcte dans ce cas même si l’erreur n’est peut-être pas importante. Enfin, les spectres d’absorption basés sur des mesures par satellite sont reconstruits par un traitement informatique dont je ne connais pas le détail. Vous en trouverez des exemples d’application sur le site http://climatemodels.uchicago.edu/models.html qui permet même de reconstruire des spectres pour différentes conditions atmosphériques.
Cher professeur,
j’ai donc pris un spectre sur le site que vous m’avez conseillé. J’ai choisi ce spectre:
http://climatemodels.uchicago.edu/modtran/
J’ai à nouveau fait mes petits quadrillages et ai calculé la surface entre 800 et 1200 1/cm, soit dans la fenêtre atmosphérique, raie de l’ozone comprise.
La surface obtenue est de 108 W/m2 soit les 36,1% du flux mesuré à une altitude de 70 km. On est bien loin des 6% (27,7 W/m2 environ dans mon cas) annoncés dans la plupart des bilans radiatifs.
Je n’ai malheureusement pas d’explication à cet écart qui paraît vraiment très conséquent!
Bonne continuation!
Ma réponse à votre avant-dernier commentaire étant imprécise je l’ai reprise mais vous n’en avez peut-être pas pris connaissance. J’y rappelais que l’émission détectée par satellite entre 8 et 13 µm (770 et 1250 cm-1) ne provient PAS exclusivement de la surface terrestre mais aussi de différentes couches atmosphériques. En effet, quel que soit le mécanisme de dissipation de l’énergie au niveau de la surface terrestre (rayonnement, convection ou évaporation de l’eau des océans) en altitude toute cette énergie doit être convertie en rayonnement car c’est le seul mécanisme permettant de l’évacuer hors du système terrestre. Les satellites peuvent observer l’atmosphère à différentes altitudes selon les canaux utilisés et il est généralement admis que chaque couche atmosphérique émet selon l’équation de Planck en fonction de sa température propre. Un traitement informatique permet alors de reconstruire un spectre global pour différentes conditions. Si, pour l’exemple que vous avez choisi, la surface mesurée correspond à 108 W m-2 la totalité est sans doute de l’ordre de 240 W m-2.
L’analogie entre les propriétés du CO2 et de la vapeur d’eau est utilisée pour conclure que la vapeur d’eau est un gaz à effet de serre bien plus efficace que le CO2, en grande partie parce que son spectre d’absorption s’étale sur de nombreuses longueurs d’onde . La théorie est toujours assez bien expliquée pour le CO2 et sa manière de transmettre l’énergie reçue par collisions avec les autres molécules de l’air, ce qui fait que l’élimination de l’énergie absorbée se dissipe en chaleur, donc en agitation moléculaire, ce qui conduit à plus de convection. Il me manque une explication sur le comportement de la molécule d’eau-vapeur activée, tenant compte du fait que l’eau a bien d’autres propriétés, notamment et surtout, elles peut devenir liquide, former des microgouttes et des nuages, modifiant aussi la facilité de laisser partir le rayonnement vers l’espace, ou au contraire, l’albedo des nuages par le dessus. Je pense qu’il serait peut-être bien qu’un physicien comme vous fasse le point.
Ce serait bien aussi que vous expliquiez comment on arrive à évaluer l’effet de serre du méthane par rapport à celui du CO2. On dit qu’il est 20 fois supérieur, mais qu’il a une durée de vie beaucoup plus courte.
Merci et bonne continuation.
Merci pour votre commentaire.
Si on qualifie de « gaz à effet de serre » toutes les molécules atmosphériques susceptibles d’absorber une fraction du rayonnement thermique de la Terre, les molécules H2O ont certainement un rôle prépondérant car leur concentration dans les basses couches atmosphériques est bien supérieure à celles de CO2 ou CH4 et leur domaine d’absorption plus étendu. De ce fait, l’absorption par la vapeur d’eau d’une fraction du rayonnement thermique de la Terre est pratiquement saturée sur une dizaine de mètres d’épaisseur atmosphérique au voisinage de la surface terrestre. Le sort de ces molécules de H2O excitées à l’état de vibration est alors semblable à celui des molécules CO2 (ou CH4) dans les mêmes conditions : elles se désactivent par collisions avec les molécules environnantes N2 et O2 sans émission d’aucun rayonnement de fluorescence. D’autre part, connaissant les spectres d’absorption de CH4 et CO2 on peut dire qu’a concentrations égales le premier absorberait plus efficacement une fraction du rayonnement thermique de la Terre mais, en réalité, sa concentration est bien inférieure à celle de CO2.
Comme vous le signalez l’eau, sous tous ses états physiques, a une influence considérable sur le climat mais cela n’a rien à voir un prétendu « effet de serre ».
Pour reprendre la remarque de Stéphane que vous n’avez manifestement pas comprise:
d’un point de vue GLOBAL le système Terre-Atmosphère n’émet de l’énergie vers l’espace QUE sous la forme radiative et les phénomènes de convection n’y jouent aucun rôle. Donc Stéphane a raison de dire que votre remarque sur l’emploi de la formule de Stefan-Boltzman est erronée. Elle est correcte pour le système global et donne une température de -18°C NON à la surface de la Terre mais à la surface moyenne d’émission vers l’espace. Puis le gradient de température dû à la pression fait que la température moyenne au sol est supérieure !!
1° Depuis la création du site http://www.science-climat-energie.be j’ai répondu à plus de 80 commentaires, positifs pour la plupart. Je n’ai pas gardé le souvenir de la remarque à laquelle vous faites allusion mais j’y ai certainement répondu en détails.
2° Prétendre que l’interlocuteur n’a pas compris le sujet abordé (mais non précisé) n’est pas une manière constructive d’aborder un débat scientifique.
3° Si vous lisez attentivement la note à laquelle vous vous référez vous comprendrez que l’atmosphère terrestre ne présente aucune des caractéristiques d’un corps noir (ou gris) : elle n’a pas de surface, les transferts énergétiques n’y sont pas exclusivement radiatifs et les constituants atmosphériques ont, en absorption comme en émission, un spectre de raies et pas un spectre continu. L’atmosphère n’émet donc aucun rayonnement thermique auquel pourrait s’appliquer la formule de Stefan-Boltzmann. Il en est de même pour le système global Terre-atmosphère que vous citez.
4° La température de -18°C mesurée à une altitude de l’ordre de 5000 m résulte de l’existence d’un gradient thermique dans l’atmosphère terrestre. Pour les raisons mentionnées ci-dessus cela n’a aucun sens de la déduire, par l’application de la formule de Stefan-Boltzmann, des 240 W/m2 mesurés par satellite.
A lire les commentaire du dénommé Stéphane et pour avoir eu les même arguments de la part d’un certain Pascal Mailier, professeur à l’UGent et chef de projet à l’IRM.
Pascal Mailier avancerait-il masqué ?
Je ne connais pas Pascal Mailier, mais dans les arguments qu’il utilise, on dirait qu’il feint de ne pas comprendre:
1e) pour son premier point, que quand le professeur Geuskens dit que le rayonnement thermique d’un corps (noir) froid ne peut être absorbé par un corps (noir) plus chaud, cela est certes mal dit (il faudrait dire: le flux net de rayonnement thermique va toujours du corps noir le plus chaud vers le corps noir le plus froid), mais il parle bien du flux net, résultant des échanges entre les 2 corps .
2e) que, si le système Terre/atmosphère pris dans son ensemble et vu de l’espace peut, dans une certaine mesure être assimilé à un corps noir ou gris, ce ne peut en aucun cas être le cas de telle ou telle tranche de l’atmosphère car d’autres phénomènes entrent en jeu (conduction, convection…)
Bonjour Professeur Geuskens,
Puisqu’il est question dans votre article du bon usage de la loi de SB, il me parait utile ici de rappeler que cette loi n’est pas une conséquence exclusive de la loi de Planck. En effet, elle a d’abord été dérivée de manière classique, par Boltzmann, bien avant la loi de Planck, bien avant la naissance de la mécanique quantique. On peut en effet dériver cette loi, de manière parfaitement rigoureuse, en partant du deuxième principe de la thermodynamique et du fait que pour un rayonnement thermique (photons), la pression est égale au tiers de la densité d’énergie. Par conséquent, dès qu’un corps à l’équilibre thermique rayonne, il y a proportionnalité entre la puissance rayonnée et la puissance 4 de la température. Et il est donc légitime d’employer la formule de SB en climatologie.
Bien à vous,
Stéphane
Merci pour votre commentaire.
Je suis d’accord avec vous à condition d’ajouter quelques précisions.
1° Oui, la formule de Stefan-Boltzmann (SB, équation (2) de l’article auquel vous vous référez) n’est pas une conséquence exclusive de l’équation de Planck (reprise sur la fig.1 du même article) pour les raisons que vous mentionnez.
2° Oui, il est légitime dans certains cas d’employer la formule de SB en climatologie à condition de faire preuve de discernement car en toute rigueur elle ne peut être utilisée que si le rayonnement thermique est le seul mécanisme d’échange énergétique. Elle ne peut donc s’appliquer globalement à la Terre où la convection de l’air et l’évaporation de l’eau des océans contribuent de manière prépondérante au bilan énergétique (voir http://www.science-climat-energie.be/2020/12/11/leffet-de-serre-et-le-bilan-energetique-de-la-terre/). Si les satellites détectent au sommet de l’atmosphère l’émission sous forme de rayonnement de 240 W m-2 on ne peut PAS en déduire, par application de la formule de SB, que la surface terrestre devrait être à la température de 255 K (-18°C) car la majeure partie de ce rayonnement ne provient PAS de la surface terrestre. De même, le fait que la température « globale moyenne » de la Terre soit 288 K (15°C) ne permet PAS d’en déduire que le flux radiatif émis par la Terre devrait être de 390 W m-2 car l’énergie reçue du Soleil est dissipée principalement par évaporation de l’eau des océans et PAS par rayonnement. Dans la conclusion de l’article cité ci-dessus je propose que dans les 240 W m-2 détectés par les satellites seulement 9 % (21 W m-2) proviendraient directement de la surface terrestre et 91 % (219 W m-2) de l’émission de fluorescence associée à la condensation de la vapeur d’eau au sommet de la troposphère.
Bonjour Professeur Geuskens,
Merci pour la réponse que vous m’avez faite le 18 septembre sous l’article « L’effet de serre et le bilan énergétique de la terre ».Je vous écris cette fois à propos de l’usage de la formule de Sterfan-Boltzmann auquel vos différents articles m’ont rendu attentif.
J’ai lu plusieurs articles sur l’effet de serre et il semble vraiment que les climatologues considèrent que la surface la terre, bien qu’entourée d’une atmosphère, rayonne comme si elle étant dans le vide, ce qui donne 390 W/m2 à 288 K. En d’autres termes, pour calculer la dissipation de l’énergie interne de la terre il faudrait utiliser un principe de superposition du rayonnement dans le vide, de la convection et de l’évaporation. La conservation de l’énergie serait rétablie par la « backradiation ». Tout ça me paraît fou. Il me semble quand même que ces modes de dissipation sont concurrents : la surface de la terre transfère son énergie par convection grâce à l’agitation de ses molécules qui entrent en collisions avec les molécules de l’atmosphère. Il me paraît que c’est cette même agitation des molécules qui émet le rayonnement thermique. Si j’ai bien compris c’est ce que vous exprimez dans cet article ?
J’ajoute qu’étant Ingénieur en Mécanique j’ai été formé au calcul de machines (moteurs, échangeurs, pompes à chaleur, etc..) utilisant les principes de la thermodynamique. A aucun moment on ne faisait recours au rayonnement dans les calculs de transferts de chaleurs et de masse (sauf aux très hautes températures). Le tout donnait un excellent accord avec l’expérience. Pourtant, dès qu’on passe dans le domaine de la climatologie, le mode radiatif devient dominant. Bizarre… Est-ce que là aussi il faut invoquer une « backradiation » qui annule les effets radiatifs des systèmes thermodynamiques?
Tout ça me paraît vraiment étrange, bien que la littérature que j’ai consultée (mais quelle est sa valeur ?) utilise sans vergogne la loi de Stefan-Boltzmann, même quand les modes de transferts de la chaleur sont multiples et simultanés. Qu’est-ce qui m’échappe ?
Cordialement.
Alain
Merci pour votre commentaire qui me permet d’attirer l’attention sur les erreurs commises par les partisans d’un « effet de serre » qui se manifesterait sous forme d’une « back radiation ».
Le rayonnement thermique d’un corps noir idéal sous vide et à l‘équilibre thermique peut être décrit par l’équation de Planck. Dans ces conditions seulement la formule de Stefan-Boltzmann qui en est dérivée peut être utilisée. Elle est bidirectionnelle : on peut déduire la température du corps émetteur à partir de la puissance émise et inversement. C’est ainsi, par exemple, que peut être déterminée la température de surface des planètes du système solaire.
En toute rigueur, l’équation de Planck et la formule de Stefan-Boltzmann ne peuvent être utilisées que si le rayonnement thermique est le seul mécanisme d’échange énergétique. Elles ne peuvent donc PAS s’appliquer à la Terre où la convection de l’air et l’évaporation de l’eau des océans contribuent de manière prépondérante au bilan énergétique. Si les satellites détectent au sommet de l’atmosphère terrestre l’émission sous forme de rayonnement de 240 W/m2 on ne peut PAS en déduire, par application de la formule de Stefan-Boltzmann, que sans « effet de serre » la température de la surface terrestre serait 255 K (-18°C). De même, le fait que la température « globale moyenne » de la Terre soit 288 K (15°C) ne permet PAS d’en déduire que sans atmosphère le flux radiatif émis par la Terre serait de 390 W/m2 et que la différence de 150 W/m2 entre ces deux valeurs serait la manifestation d’une « back radiation » due au CO2.
Comme je l’explique dans la note http://www.science-climat-energie.be/2020/12/11/leffet-de-serre-et-le-bilan-energetique-de-la-terre/ seulement 6 % des 240 W/m2 détectés par les satellites proviennent directement de la surface terrestre, le reste provient des couches supérieures de la troposphère à des températures bien plus basses. D’autre part, la surface terrestre ne reçoit que 50 % des 342 W/m2 apportés par le rayonnement solaire au sommet de l’atmosphère et, pour maintenir son équilibre thermique, ne devrait PAS dissiper 390 W/m2 mais seulement 171 W/m2.
Pourquoi cette polarisation sur les transferts radiatifs ?
Parce que le système Terre-Atmosphère étant, au sens de la thermodynamique, un système « fermé » ne peut échanger que du rayonnement avec le reste de l’univers. Le problème fondamental, si on s’intéresse au bilan énergétique du système Terre-Atmosphère, est : par quel mécanisme ? Certains climatologues utilisent encore une fois l’équation de Stefan-Boltzmann en assimilant des molécules individuelles à des corps noir. J’ai évoqué ce problème en réponse à un de vos précédent commentaire. Je pense que c’est une erreur et je formule une autre hypothèse au paragraphe 4.3 de la référence ci-dessus (Origine du rayonnement détecté par satellites).
Merci professeur pour votre réponse.
J’ai encore une question : certains ont donné comme illustration du problème de répartition de la dissipation de chaleur entre rayonnement et convection les sondes Pirani utilisées pour la mesure de pression dans la technique du vide. Dans ce cas particulier, la convection évacue nettement mieux la chaleur que le rayonnement. Ils y voient une preuve qu’on ne peut pas utiliser l’équation de Stefan-Boltzmann pour le système terre-atmosphère . Pensez-vous que c’est une bonne analogie?
Cordialement.
Alain Hess
L’analogie ne me semble PAS valable car les jauges de Pirani ont été conçues spécifiquement pour mesurer la variation de conductivité d’un mince filament en fonction de la fréquence des collisions avec les molécules du gaz dont on veut mesurer la pression. Pour limiter le rayonnement le filament est très mince et n’est pas incandescent.
Outre les limitations à l’usage de la formule de Stefan-Boltzmann rappelées dans ma réponse à votre précédent commentaire il est évident qu’elle ne peut PAS s’appliquer à des molécules individuelles puisque, comme l’équation de Planck, elle concerne l’émittance hémisphérique à partir d‘une surface.
Merc pour votre réponse, Profeseur
Un autre question que je me pose : si la terre avait une atmosphère sans gaz à effet de serre (et donc sans océans, mers, lacs..), que se passerait-il?
On peut imaginer que l’atmosphère serait transparente au rayonnement, autant visible qu’infrarouge. Toutefois, il y aurait également une partie de l’énergie reçue du soleil qui serait dissipée par convection et finirait par s’élever en altitude donnant lieu à une circulation dans l’atmosphère. Il faudra bien trouver un moyen d’évacuer cette chaleur vers l’espace pour que l’atmosphère se stabilise à une température d’équilibre. Or, comment faire puisque l’azote et l’oxygène ne rayonnent qu’à de plus hautes fréquences? Est-ce que le moyen ne serait pas que l’atmosphère se réchauffe et transmette cette chaleur par conduction à la terre qui elle-même se réchaufferait, reproduisant ainsi un simili « effet de serre »?
Qu’en pensez-vous?
Meilleures salutations.
Alain Hess
Merci pour votre réponse.
Effectivement je pensais à la vapeur d’eau et au CO2 et faisait évidemment abstraction du développement de la vie puisque le cas imaginé est complètement hypothétique.
Merci pour tous ces articles et échanges qui donnent sérieusement à réfléchir. Si cette science acceptait la discussion et la contradiction, tous ces doutes auraient levés depuis longtemps et, pour avoir pas mal cherché, j’ai vraiment l’impression que ce n’est pas le cas et que les fondations de cette science du climat sont bien fragiles.
Cordialement.
Avez-vous entendu parler de la théorie MEGA – Modèle d’Espace Granulaire Animé ? Cette théorie trouverait sa place en amont de la Relativité et de la Mécanique quantique et semble prétendre pouvoir les unifier. Et elle est, curieusement, assez simple.
Elle explique la gravitation, et conteste l’existence de la matière noire.
Elle justifie le spectre du rayonnement cosmique sur la base d’une interprétation de la loi de Planck ne faisant pas appel aux probabilités.
Elle propose une interprétation nouvelle de E=mc².
Tout ce qui y est dit serait vérifiable.
J’aimerais en discuter. Critiques ? Réfutation ?…
Site : http://www.kbj-modele.fr
Merci pour votre commentaire auquel je n’ai rien à ajouter car je ne suis pas compétent pour discuter de la théorie MEGA