Le forçage radiatif (radiative forcing) peut être défini comme la différence entre l’énergie radiative reçue du Soleil et l’énergie radiative émise vers l’espace par la Terre. Ce concept a été introduit par les  partisans d’un réchauffement climatique d’origine anthropique pour donner une base quantitative à la théorie de l’effet de serre défini comme « un phénomène radiatif causé par des gaz tels la vapeur d’eau ou le CO₂ qui absorbent une fraction du rayonnement infrarouge émis par la Terre et le réémettent ensuite dans toutes les directions et notamment vers la surface terrestre dont la température serait, de ce fait, plus élevée qu’en l’absence de gaz absorbant l’infrarouge».

Le forçage radiatif ∆F dû au CO₂ correspond donc à la fraction du rayonnement thermique de la Terre qui serait absorbée par ce gaz puis réémise vers la Terre. Il en résulterait une perturbation du bilan énergétique de la Terre dont la température devrait, selon les  partisans d’un réchauffement climatique d’origine anthropique, augmenter pour dissiper plus d’énergie par rayonnement thermique afin d’atteindre un nouvel équilibre.

La version la plus récente de la formule semi-empirique utilisée par le GIEC pour lier le forçage radiatif à la teneur en CO₂ dans l’atmosphère provient d’un article de G. Myrhe et coll. paru en 1998 dans Geophysical Research Letters (vol 25, p. 2715) et intitulé « New estimates of radiative forcing due to well mixed greenhouse gases » :

∆F (W m^-2) = 5,35 ln C/C₀                               (1)

Dans cette formule C est la concentration du CO₂ en ppmv  (parties par million en volume) à un moment donné et C₀  la concentration de référence, par exemple avant le début de l’ère industrielle (278 ppmv). Elle est obtenue en introduisant des teneurs en CO₂ extrapolées jusqu’à 1000 ppmv dans plusieurs modèles climatiques globaux sans tenir compte d’un effet de saturation de l’absorption qui interviendra nécessairement avec l’augmentation de la teneur en CO₂. Les résultats sont rassemblés sur la fig. 1 extraite de l’article cité. La relation (1) décrit l’allure de ces courbes.

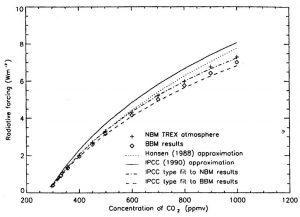
 Fig. 1 Forçage radiatif en fonction de la concentration en CO2 (d’après Myrhe 1998)

En 2005 le forçage radiatif depuis le début de l’ère industrielle était estimé par le GIEC à 1,7 W m^-2 mais actuellement avec une teneur en CO₂ dans l’atmosphère proche de 400 ppmv la valeur déduite de la formule (1) serait de 2 W m^-2.

Il faut remarquer que la publication de Myrhe date de 1998 et correspond à une période allant approximativement de 1980 à 2000 pendant laquelle les  partisans d’un réchauffement climatique d’origine anthropique ont voulu établir une corrélation entre l’augmentation de température moyenne globale (fig. 2) et l’augmentation de la teneur en CO₂ dans l’atmosphère. Cependant  depuis près de 20 ans la température ne varie pratiquement plus (fig. 3), bien que la teneur en CO2 n’ait cessé d’augmenter d’environ 2 ppmv par an.

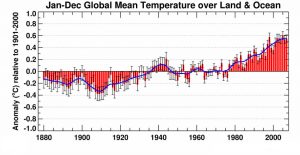
Fig. 2  Ecarts de température pour la période 1880-2015 par rapport à la moyenne  pour la période 1901-2000 (en rouge moyennes annuelles, en bleu courbe lissée)

Le problème est d’établir un lien entre le forçage radiatif estimé d’après la formule (1) et l’augmentation de température qui en résulterait selon la théorie de l’effet de serre. A cet effet les climatologues se basent toujours sur la formule de Stefan Boltzmann qui lie la puissance rayonnée par unité de surface F à la température T (en K)  à la puissance  4 :

F (W m^-2)  = σ T⁴ (σ = constante de Stefan = 5,67 x 10^-8 W m^-2 K^-4)

Si le CO₂ donne lieu à un forçage radiatif estimé à 2 W m^-2 ils considèrent que la température de la Terre devrait nécessairement augmenter pour dissiper sous forme de rayonnement thermique ce surcroît d’énergie reçue. Or, il est bien établi que deux autres mécanismes contribuent également, et de manière prépondérante,  à la dissipation de l’énergie par la Terre : la convection de l’air et l’évaporation de l’eau des océans. La formule de Stefan Boltzmann sous la forme mentionnée ci-dessus n’en tient pas compte.

Certains climatologues écrivent néanmoins sur la base de la formule de Stefan Boltzmann :

T⁴ (actuel) / T⁴ (préindustriel) = F + ∆F / F                          (2)

Si  la puissance F rayonnée au sommet de l’atmosphère était de 240 W m^-2 au début de l’ère industrielle et si le forçage radiatif ∆F est aujourd’hui  de 2 W m^-2 le rapport des F vaudrait 242/240 = 1,008 et le rapport des T = 1,002. On en déduit que si la température était 288 K au début de l’ère industrielle elle deviendrait 288,6 K aujourd’hui  soit une augmentation de température de 0,6 °C. Une méthode différente utilisée par d’autres climatologues est basée cette fois sur la dérivée de la formule de Stefan Boltzmann qui pourrait s’écrire :

dF/dT = 4 σ T³ d’où  ∆F = 4 σ T³ ∆T                           (3)

 Avec un forçage radiatif de 2 W m^-2 et si la température était 288 K au début de l’ère industrielle on trouve cette fois ∆T = 0,37 °C.

En réalité la fig. 2 montre que l’augmentation globale de température enregistrée depuis 1880 ne suit ni l’une ni l’autre des relations (2) et (3).  Elle est globalement de 0,7 °C mais passe par un minimum en 1910 suivi d’un petit maximum en 1940, d’un palier de 1950 à 1980 et d’une remontée à partir de 1980 pour se stabiliser depuis l’an 2000 approximativement.

La sensibilité climatique est définie comme l’augmentation de température qui résulterait d’un doublement de la concentration en CO₂ pour atteindre 800 ppmv (en 2200 au taux de croissance actuel). La valeur trouvée serait comprise entre 0,7 et 1,4 °C sur la base des relations (2) ou (3) donc de l’ordre de 1°C par rapport à aujourd’hui. Ce n’est pas très important mais des rétroactions positives peuvent amplifier cet effet. On peut faire intervenir, par exemple, la vapeur d’eau, autre gaz à « effet de serre », dont la concentration augmenterait suite à l’élévation de température ou la fonte de la banquise et la diminution des surfaces enneigées qui auraient pour effet de diminuer l’albédo de la Terre et donc la fraction d’énergie solaire réfléchie. Pour une revue d’une douzaine de possibilités de rétroactions positives voir ici.

Pour calculer la sensibilité climatique une formule censée tenir compte de différentes rétroactions  est proposée ici :

∆T =  0,8 ∆F                                             (4)

 Avec ∆F = 3,7 W m^-2 calculé par la formule (1) pour un doublement de la concentration en CO₂ la formule (4) conduit à une augmentation de température de 3 °C,  valeur adoptée par la National Academy of Sciences (Washington) en 1979 avec une marge d’erreur de 1,5 °C selon l’importance relative attribuée aux diverses rétroactions  dans différents modèles climatiques globaux.

Il est évident que l’intervention de divers types de rétroaction  permet l’introduction de nombreux paramètres dans différents modèles climatiques globaux. Dès lors tous les ajustements sont possibles entre la réalité climatique et les modèles théoriques comme l’illustre la fig. 3.

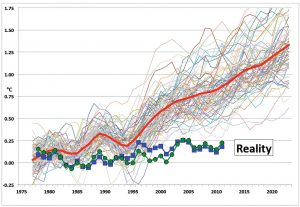
Fig. 3  Ecarts de températures par rapport à 1975 (moyenne des mesures par ballons-sondes en vert ,  par satellites en bleu) et prédictions selon différents modèles climatiques (ligne rouge = moyenne de 102 modèles)