Carbone 14 et Effet Suess

par J.C. Maurin, Professeur agrégé de physique

Une croissance du CO₂ atmosphérique qui serait exclusivement anthropique est contradictoire avec les observations du carbone 13 dans l’atmosphère (ici). Cet article en 3 parties va montrer qu’il existe également des contradictions avec les observations du carbone 14. Celui-ci  est utilisé à des fins de datation jusqu’à 50 000 ans BP  (Before Present) et on dispose de nombreuses études (pour calibration) sur son évolution dans l’atmosphère.  

La première partie s’intéresse, non pas aux datations, mais à la dilution du carbone 14 que provoque l’ajout de CO₂ anthropique (effet SUESS)  avant les essais thermonucléaires de 1952-1963.
Dans la seconde partie nous verrons que l’évolution du carbone 14 après 1963 est aussi en contradiction avec une croissance du CO₂ exclusivement anthropique.

1. Le carbone dans l’atmosphère [1] [5]

Le carbone existe habituellement sous 3 formes isotopiques : ¹²C pour ≈ 98.9% , ¹³C pour ≈ 1.1 % et ¹⁴C à l’état de traces (Fig. 1a).

 

Figure 1a.  La seule différence entre CO₂ anthropique et CO₂ atmosphérique réside dans les proportions du mélange des isotopes: le CO₂ anthropique est appauvri en ¹³C et ¹⁴C.  L’ajout de CO₂ anthropique va modifier, au fil des années, les proportions du mélange isotopique dans l’atmosphère.

Le carbone 14 n’est pas stable : sur 1000  atomes ¹⁴C, il en subsiste ≈ 500 après 5730 ans (= période de demi-vie, Fig. 1b).

Figure 1b. [5] Désintégration de l’isotope 14 du carbone. La décroissance est  proportionnelle au nombre d’atomes subsistants.  

Pourquoi reste-t-il encore aujourd’hui du carbone 14?  La raison se trouve dans l’existence d’un flux de neutrons cosmiques qui interagissent avec l’azote dans la haute atmosphère pour former ¹⁴C (¹⁴N +n →¹⁴C+1p).  Le ¹⁴C va s’oxyder rapidement pour donner la molécule ¹⁴CO₂  (dioxyde de carbone avec carbone = ¹⁴C).

• Si le flux de neutrons cosmiques est presque constant à l’échelle du siècle, alors un niveau d’équilibre dynamique doit s’établir : la production en 100 ans de ¹⁴C en haute atmosphère compense la disparition en 1 siècle (-1,2%) du ¹⁴C.
  Au cours des derniers siècles, cet équilibre dynamique correspond à environ 1 molécule ¹⁴CO₂ pour 10¹² molécules ¹²CO₂.
• Le carbone végétal ou animal trouve sa source dans le CO₂ atmosphérique. Le ¹⁴CO₂ sera lui aussi incorporé dans la matière organique. Il y a, à terme, équilibre dynamique entre carbone 14 de l’atmosphère et carbone 14 de la matière organique par recyclage du carbone. Le rapport ¹⁴C /¹²C va diminuer après la mort de l’organisme car il n’y a plus d’apport de ¹⁴C.
  L’idée d’utiliser cette décroissance pour datation « carbone 14 » est due à W.F.Libby (1946).

Les études pour calibration des datations ont montré, que d’une part, l’homme modifie le rapport ¹⁴C /¹²C dans l’atmosphère, et, d’autre part, le passage du carbone depuis le CO₂ atmosphérique vers la biosphère conduit à un fractionnement isotopique (la végétation sélectionne le ¹²C de préférence au ¹⁴C).

Figure 1c. [5] On évalue la proportion de ¹⁴C en mesurant l’écart par rapport à une référence étalon. Pour des raisons pratiques, la mesure est adaptée afin d’obtenir une grandeur normalisée Δ ¹⁴C usuellement exprimée en ‰.

Par commodité, on a fixé Δ ¹⁴C = 0‰  pour l’équilibre : production par les neutrons cosmiques en haute atmosphère = disparition par désintégration (Fig. 1c).  Avant 1850 on a Δ ¹⁴C = 0‰, l’homme n’influait alors quasiment pas sur le CO₂ atmosphérique.
En l’absence totale de ¹⁴C, le CO₂  est tel que Δ ¹⁴C = -1000 ‰. C’est le cas du CO₂ produit par les combustibles fossiles, formés il y a plusieurs millions d’années, et qui ne comportent donc plus de ¹⁴C (voir Figs. 1a et 1b).

2. Evolutions du carbone 14 dans l’atmosphère

La reconstitution de la Fig. 2 résume les observations sur ¹⁴C.

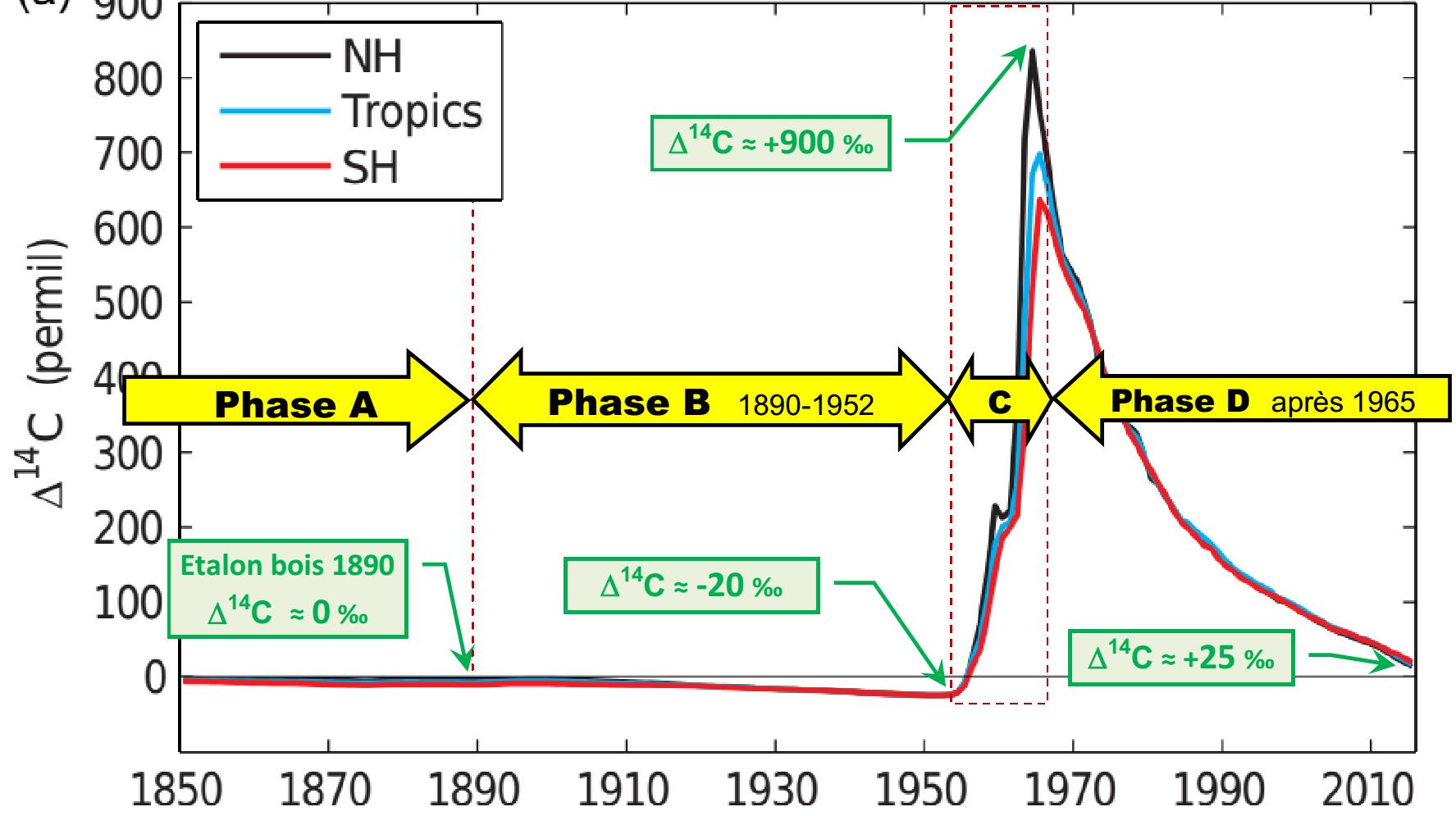
Figure 2.  (d’après la Fig.1 ici). Reconstitution de  Δ ¹⁴C pour l’atmosphère depuis 1850.
La désintégration du carbone 14 est presque négligeable à l’échelle du siècle  (-1.2% selon Fig.1b). On  distingue 4 phases A, B, C et D.

Phase A.   La production de ¹⁴C par les neutrons cosmiques équilibre la désintégration du stock total de ¹⁴C  →  Δ¹⁴C  ≈ 0 ‰.

Phase B. L’atmosphère s’appauvrit en ¹⁴C : on passe de Δ¹⁴C ≈ 0 ‰ en 1890 vers ≈ -20‰ en 1950. Cette phase B fait l’objet du présent article.

Phase C.  L’explosion d’une bombe H produit un flux de neutrons. Ces neutrons vont créer, à partir de l’azote atmosphérique l’isotope ¹⁴C en grande quantité. Dans l’atmosphère, ¹⁴C s’oxyde rapidement pour donner ¹⁴CO₂. Lors des essais des armes thermonucléaires (à partir de 1952), Δ¹⁴C passe de -20 ‰vers + 900 ‰.  Le tableau (Fig. 1c) indique que l’atmosphère en 1963 comporte presque 2 fois plus de molécules ¹⁴C que l’atmosphère en 1952.

Phase D.  A la fin 1965, ¹⁴CO₂ s’est réparti presque également dans les 2 hémisphères.
Le nombre de molécules ¹⁴CO₂  dans l’atmosphère décroît rapidement (en 2015 on est proche du niveau d’équilibre de 1950).

Cette phase D (désignée par « effet Bombe ») sera étudiée dans l’article à suivre.

3. Etude de la phase B (effet Suess)

Dans un article de 1955, Hans SUESS [2], avance l’idée que l’injection de CO₂ anthropique (Δ¹⁴C  = -1000 ‰) est la cause essentielle de la baisse du Δ¹⁴C  depuis ≈ 0 ‰  en 1890 vers ≈ -20 ‰ en 1950 pour le CO₂ atmosphérique (Fig. 3).

Cet effet de dilution est souvent désigné par « effet SUESS ». Il est toutefois nécessaire de supposer un flux neutronique peu variable dans la haute atmosphère entre 1890 et 1950.

 

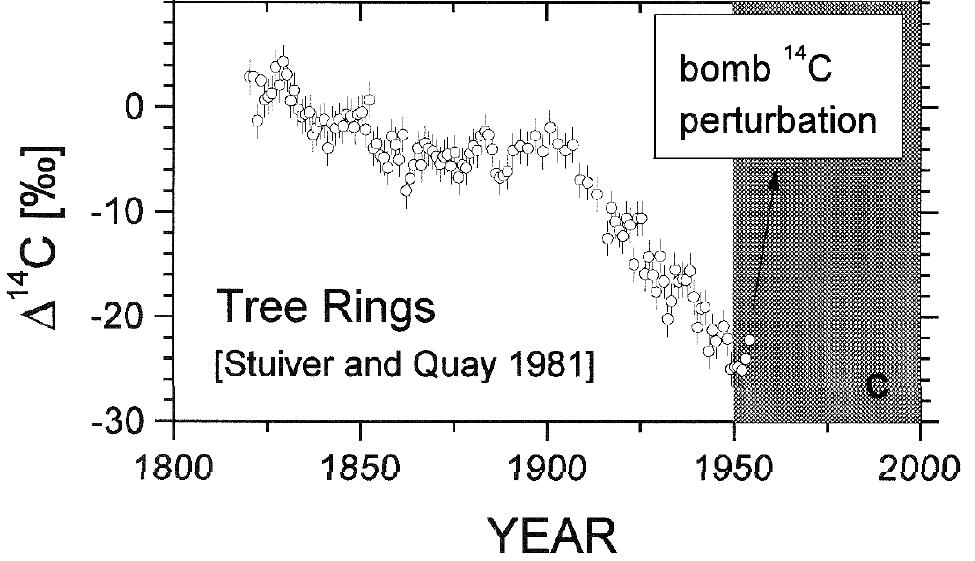
Figure 3. [2] Stuiver et Quay (1981) rapportent une proportion de ¹⁴C presque constante jusqu’en 1900 et qui baisse ensuite vers  Δ¹⁴C ≈  – 25 ‰ en 1950. L’estimation de Δ¹⁴C pour l’atmosphère est déduite indirectement via des échantillons anciens de bois qui présentent des variations suivant la localisation géographique. L’activité est faible, ce qui rend la mesure délicate (≈ 14 désintégrations par minute pour 1 gramme de carbone). Selon Tans, De Jong, Mook (1979),  on a Δ¹⁴C entre  – 15 ‰   et – 25 ‰. Dans la suite de l‘article, nous utiliserons Δ¹⁴C ≈  – 20 ‰ . 

Un étang salé dans lequel l’homme vient ajouter de l’eau douce présente une analogie avec l’effet Suess : la salinité de l’étang correspond à Δ¹⁴C, l’eau douce correspond  au CO₂ anthropique, l’étang salé correspond à l’atmosphère. L’effet Suess est alors analogue à la baisse de salinité de l’étang en fonction de la quantité d’eau douce ajoutée par l’homme. L’analogie est meilleure si on imagine un étang qui communique avec la mer car l’atmosphère échange avec d’autres réservoirs.

4. Thèse du GIEC

Une croissance du CO₂ atmosphérique qui serait exclusivement anthropique constitue la thèse défendue par divers organismes intergouvernementaux, tels que le GIEC ou son co-créateur l’OMM (Organisation Météorologique Mondiale).

Les figures 4a 4b 4c  illustrent l’équivalence avec l’autre formulation du GIEC « airborne fraction ≈ 55% » (ce qui signifie qu’environ la moitié des émissions anthropiques s’accumuleraient dans l’atmosphère (voir la définition de ‘airborne fraction’ dans [4]).

 

Figure 4a.   Croissance du CO₂ mesurée à Mauna Loa (MLO) [5] [3].  Le cumul anthropique (courbe rouge) est la somme, année par année, des émissions fossiles.  La comparaison entre 100% de cumul du CO₂ anthropique et la croissance du CO2 atmosphérique mesurée à Mauna Loa (MLO) montre que les émissions anthropiques ne demeurent pas  en totalité dans l’atmosphère (airborne fraction doit être < 100%).

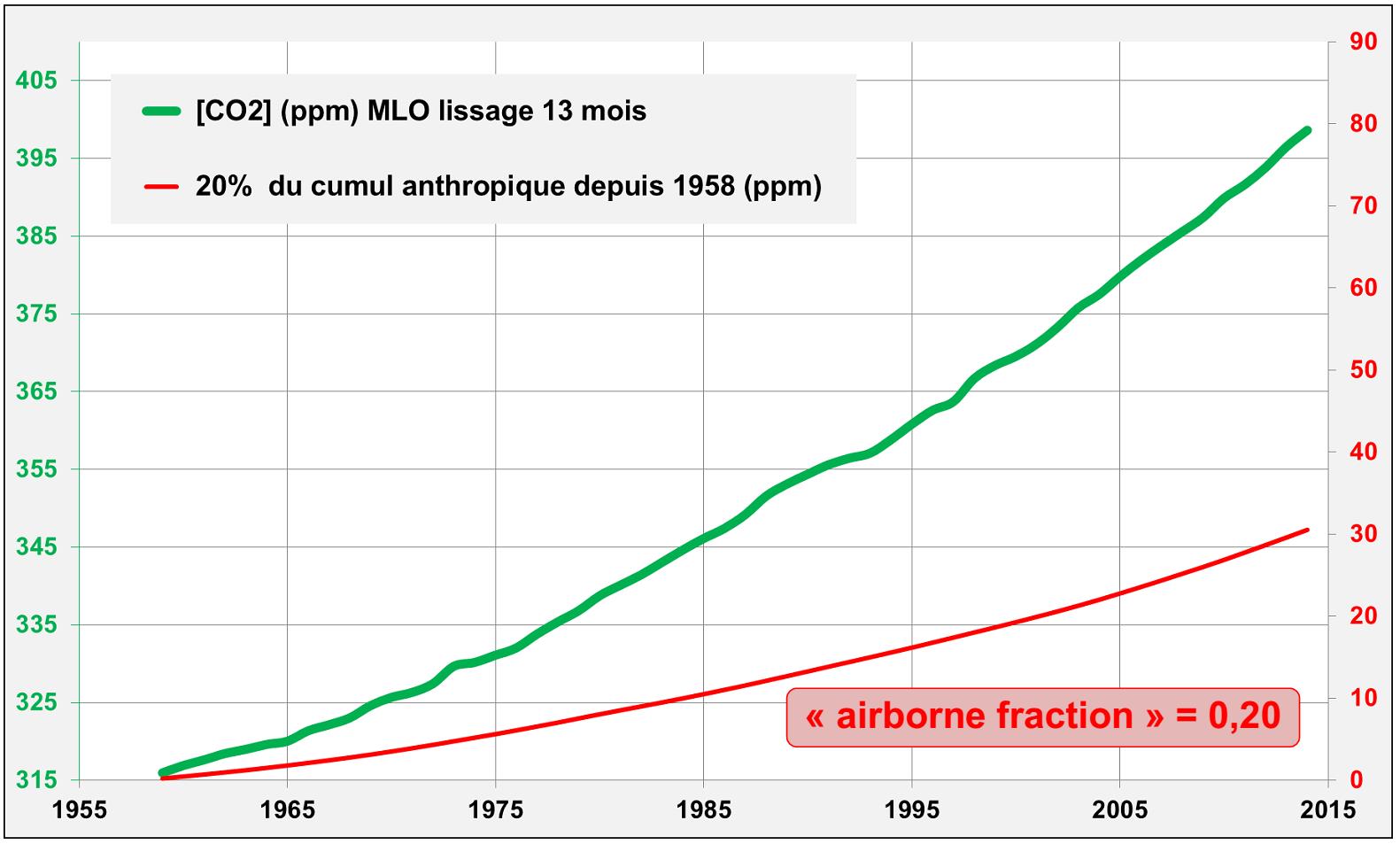
Figure 4b. [5] [3]    En prenant airborne fraction = 20%, on ne reproduit qu’une fraction de la croissance mesurée à Mauna Loa (MLO) entre 1958 et 2015 (airborne fraction doit être > 20%).

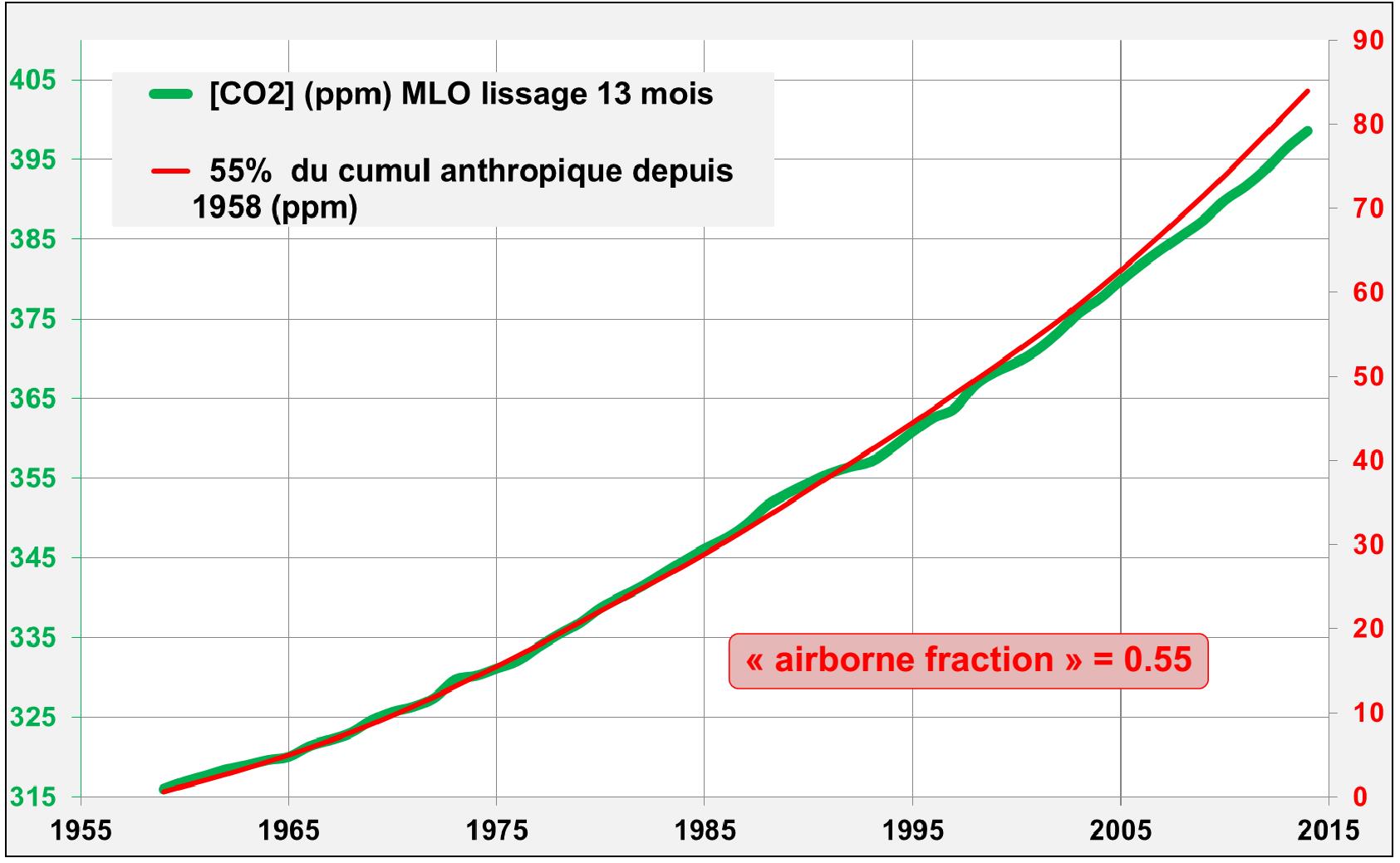
Figure 4c.[5] [3] [4] En prenant airborne fraction = 55%, on reproduit presque la croissance mesurée à MLO entre 1958 et 2015. Ceci constitue la thèse du GIEC, mais on suppose alors implicitement que seules les émissions anthropiques expliqueraient la croissance du CO₂ atmosphérique.

A propos de la corrélation entre les 2 courbes de la Fig. 4c, on peut consulter l’article de Jamal Munshi [4] dont voici la conclusion : « We find that detrended correlation analysis of annual emissions and annual changes in atmospheric CO2 does not support the anthropogenic global warming hypothesis because no evidence is found that changes in atmospheric CO2 are related to fossil fuel emissions at an annual time scale. » 

Quelle était la quantité de CO₂ anthropique, selon la thèse du GIEC, dans l’atmosphère de 1950 ? (Fig. 4d).

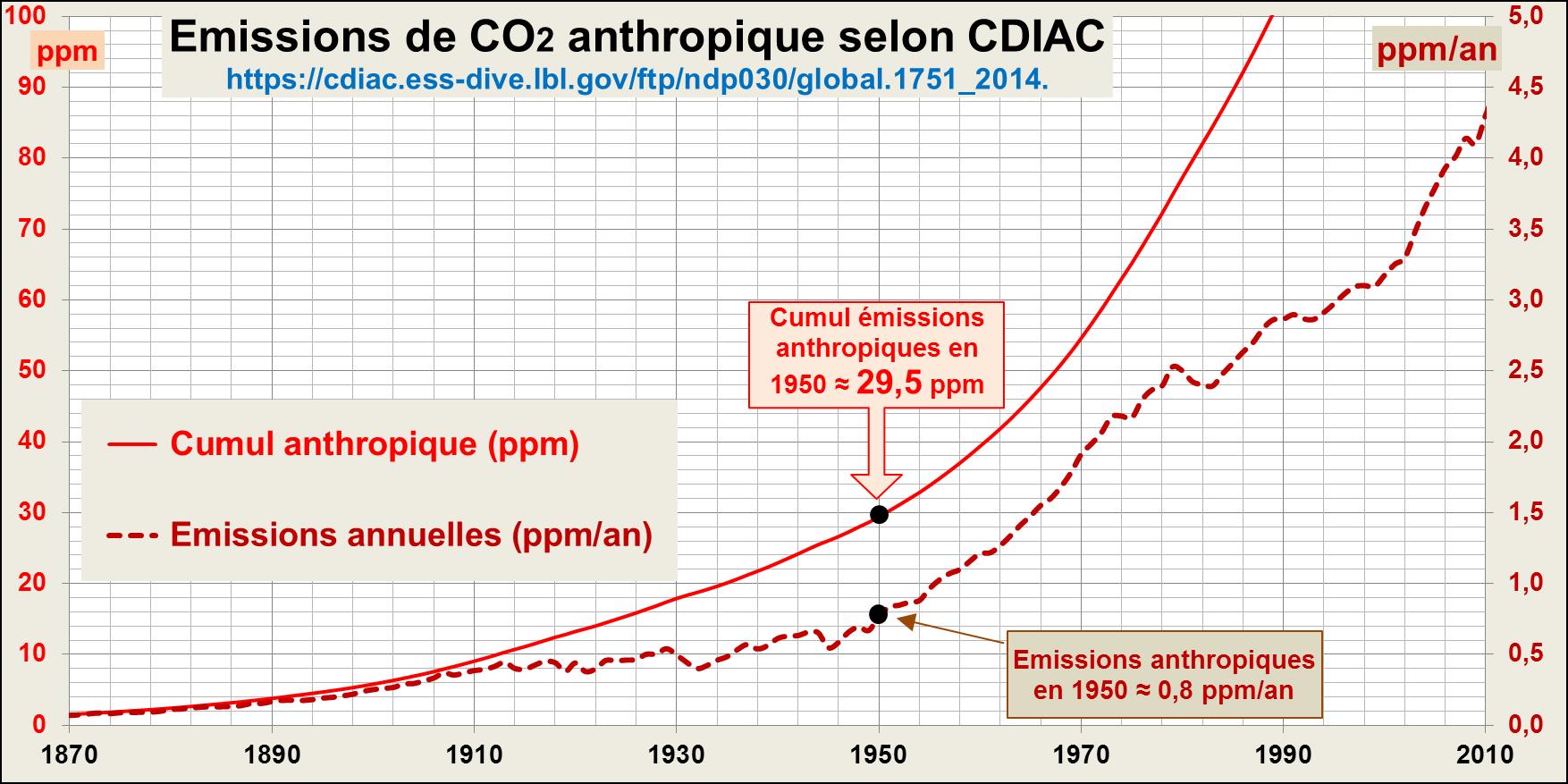
Figure 4d. [3] Emissions et cumul du CO₂ anthropique selon CDIAC. En 1950 le cumul est ≈ 29.5 ppm. Selon le GIEC, on devrait donc avoir 29.5* 55%  ≈ 16.2ppm de CO₂ anthropique (Δ¹⁴C  = -1000 ‰) dans l’atmosphère de 1950 [5]  cfr. onglet émissions CDIAC.

Le paragraphe suivant examine les conséquences, vis-à-vis de l’effet Suess, de la présence de 16.2 ppm de CO₂ anthropique (airborne fraction = 55%) dans l’atmosphère de 1950.

5. Calcul de l’effet Suess selon la thèse du GIEC

Cette valeur de 16.2 ppm de CO₂ anthropique permet-elle d’expliquer l’effet SUESS en 1950? Les archives glaciaires [3] indiquent une atmosphère en 1950 telle que [CO₂] ≈ 311 ppm. Une estimation de l’effet Suess devrait donner :
Δ¹⁴C ≈ (16.2 * -1000 ‰ + 294.8 * 0 ‰) / 311 ≈ – 52 ‰  mais les observations pour 1950 donnent Δ¹⁴C ≈ – 15 ‰ à -25‰ (Fig. 5a).

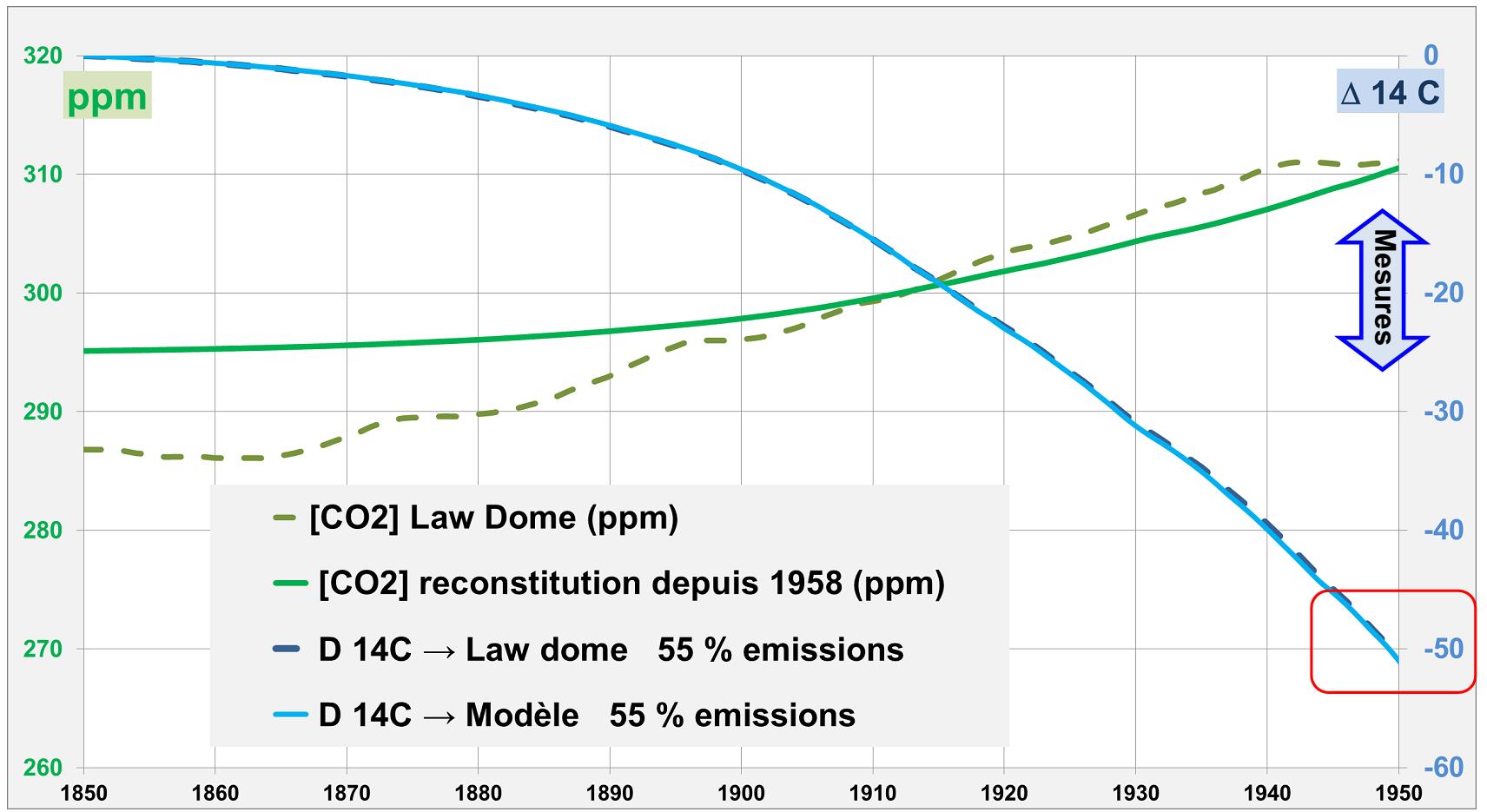
Figure 5a. [3]. La feuille de calcul [5] cfr. onglet Calcul effet Suess permet de déterminer, année par année, l’évolution du Δ¹⁴C. Le flux de neutrons cosmiques est supposé peu variable entre 1850 et 1950. La [CO₂] entre 1850 et 1950 ne peut provenir des mesures à Mauna Loa (MLO) qui démarrent seulement en 1958. La [CO2] est donc, soit déduit des archives glaciaires à  Law Dome (pointillé vert), soit reconstitué à partir de 1958 MLO (vert).
Dans les 2 cas, le calcul de Δ¹⁴C (courbes bleues) donne une valeur proche de l’estimation précédente c’est-à-dire que la dilution est bien trop grande (Δ¹⁴C  ≈ -52 ‰ à la place de -15 ‰  à -25‰ pour les observations). 

La thèse du GIEC (accumulation dans l’atmosphère d’environ la moitié des émissions anthropiques ou airborne fraction ≈ 55%) donne donc une baisse du Δ¹⁴C  nettement plus élevée  que ce qu’indiquent les observations entre 1890 et 1950. En poursuivant l’analogie avec l’étang salé, la quantité d’eau douce selon le GIEC est trop grande pour la salinité mesurée dans l’étang. Remarque : une contradiction similaire existe également pour le ¹³C (voir ici, paragraphe C.3.1).

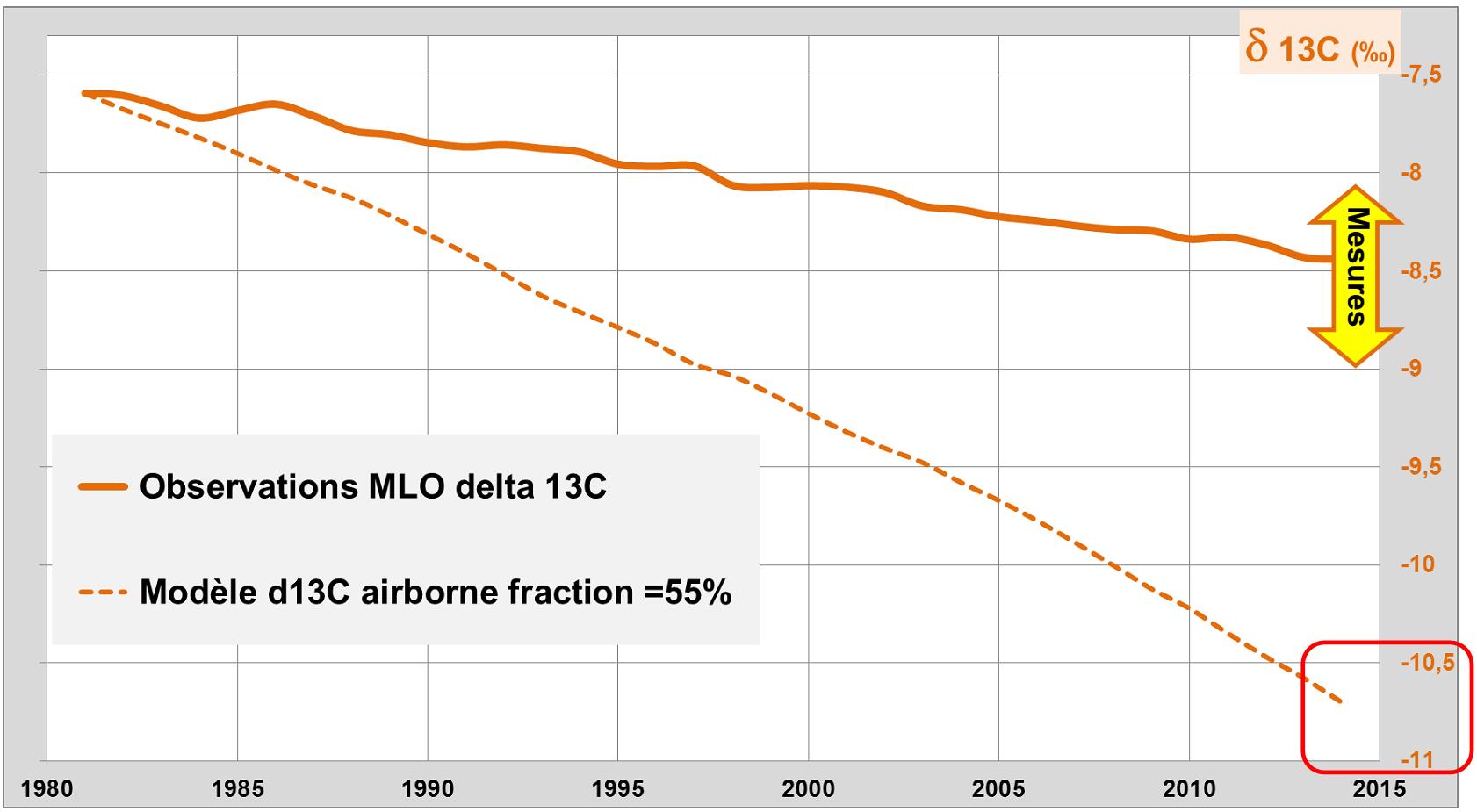
 Figure 5b. La dilution est trop grande également pour ¹³C. La thèse du GIEC (airborne fraction = 55%) donne aussi une baisse du δ¹³C nettement plus élevée que les observations. 
Afin de concilier les observations, on peut prendre airborne fraction = 24% et des apports nets naturels tels que δ¹³C ≈-0.5 ‰  [5] cfr. onglet calcul delta 13C.

6. La croissance du CO₂ atmosphérique est-elle uniquement anthropique ?

Comment concilier la dilution du CO₂anthropique en 1950 (effet SUESS) pour être en accord avec Δ¹⁴C ≈ – 15 ‰.à -25 ‰ ?  Si on écarte une forte augmentation du flux neutronique entre 1890 et 1950, il est nécessaire d’avoir une airborne fraction plus faible.
Avec 21% du cumul soit 29.5*0.21 ≈ 6.2 ppm de CO₂anthropique, on trouve Δ¹⁴C ≈ (6.2 * -1000 ‰ + 304.8 * 0 ‰) / 311 ≈ – 20 ‰ (Fig. 6a).

Figure 6a. [3] On reproduit dans l’encadré en noir les estimations de Stuiver & Quay (1981). La feuille de calcul [5] permet une estimation plus précise (année par année) de l’évolution du Δ¹⁴C (avec un flux neutronique peu variable entre 1890 et 1950).
Les valeurs utilisées pour [CO₂] entre 1850 et 1950 sont identiques à celles de la Fig.5a. 
A condition de considérer 6.2 ppm soit un cumul de 21% (airborne fraction) des émissions anthropiques (courbe rouge), on retrouve la valeur Δ¹⁴C ≈ – 20 ‰.  (courbe bleue).

Le tableau (Fig. 6b) ci-dessous indique la quantité de CO₂  anthropique qui doit être présente dans l‘atmosphère de 1950, pour obtenirΔ¹⁴C ≈ – 15 ‰.à -25 ‰.

 

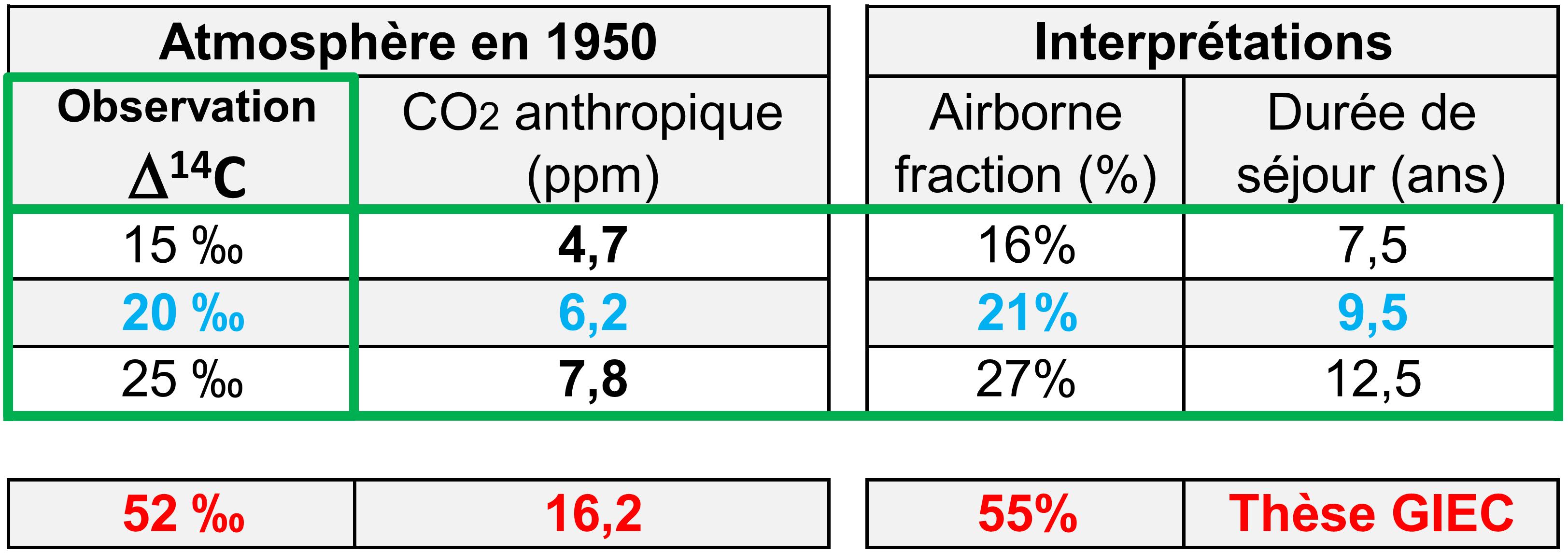
Figure 6b.   Correspondance CO₂ anthropique avec  Δ ¹⁴C. On retrouve la valeur Δ¹⁴C ≈ – 20 ‰ à la condition d’avoir 6.2 ppm de CO₂  anthropique dans l’atmosphère de 1950. Cette valeur de 6.2 ppm peut s’interpréter de 2 manières :
– Airborne fraction→ 6.2 ppm = 21% du cumul de toutes les émissions anthropiques depuis l’origine.
– Durée de séjour→ 6.2 ppm = cumul des émissions anthropiques des 9.5 années précédentes  [5 ], cfr. onglet émissions CDIAC.

La durée de séjour est définie comme le rapport   [CO₂](ppm) / Sortie(ppm/an).
Avec cette interprétation, le CO₂ (anthropique ou naturel) de l’atmosphère serait renouvelé en 9.5 ans. A partir de l’effet Suess de 1950, on peut donc également estimer une durée de séjour du CO₂ dans l’atmosphère: celle-ci doit être comprise approximativement entre 7 ans et 13 ans afin de concilier les observations Δ¹⁴C ≈ – 15 ‰  à -25 ‰ . Après 1952, les essais nucléaires ne permettent malheureusement plus de comparaison directe de l’effet Suess avec la thèse du GIEC.

7. Conclusions

1/ Une croissance exclusivement anthropique du CO₂ atmosphérique ne peut expliquer la baisse du Δ¹⁴C dans l’atmosphère entre 1890 et 1950, à partir du seul effet Suess et pour un flux de neutrons peu variable;

2/ Plus généralement, une croissance exclusivement anthropique semble peu conciliable avec les 2 observations suivantes :
Δ¹⁴C passe de ≈ 0 ‰ en 1890 vers -15 ‰ à -25‰  en 1950, δ¹³C passe de -7.6 ‰ en 1980 vers -8.3 ‰  en 2010  (voir ici, paragraphe C.3.1);

3/ L’abandon d’une origine exclusivement anthropique pour la croissance du CO₂ atmosphérique permet de concilier ces 2 observations Δ¹⁴C et δ¹³C;

4/ L’effet Suess en 1950 permet également une estimation indirecte de la durée de séjour : entre 7 et 13 ans.

Les valeurs obtenues dans le présent article sont des estimations hautes, car d’autres sources appauvries  en carbone 14 existent (volcanisme par exemple).

La phase D (effet Bombe) sera examinée dans l’article à suivre et sera confrontée à la thèse du GIEC.

Partie 2/3 de l’article (Carbone 14 et effet bombe)

Partie 3/3 de l’article (Effet bombe et modèles du GIEC)

8. Références

[1]. Carbone 14, Fiche IRSN;Radiocarbon Determination

[2]. Effet Suess
E. Suess 1955. Radiocarbon Concentration in Modern Wood, Science, vol. 122, n^o3166,‎ (DOI 10.1126/science.122.3166.415-a)
Stuiver & Quay 1981. https://www.sciencedirect.com/science/article/pii/0012821X81900406?via%3Dihub
Tans, De Jong & Mook 1979.   https://www.nature.com/articles/280826a0
Jean-Baptiste, M. Paterne 2003.DOI: 10.105l/radiopro:2003017

[3].  Données CO₂
Emissions anthropiques   CDIAC.
[CO₂] après 1958 :
ftp://aftp.cmdl.noaa.gov/products/trends/co2/co2_annmean_mlo.txt
[CO2] avant 1958 :   ftp://ftp.ncdc.noaa.gov/pub/data/paleo/icecore/antarctica/law/law2006.txt

[4]. Thèse GIEC sur le cumul anthropique dans l’atmosphère.

AR4 WG1 Chap 2 page 139  « The relationship between increases in atmospheric CO2 mixing ratios and emissions has been tracked using a scaling factor known as the apparent ‘airborne fraction’, defined as the ratio of the annual increase in atmospheric CO2 to the CO2 emissions from annual fossil fuel and cement manufacture combined (Keeling et al., 1995). On decadal scales, this fraction has averaged about 60% since the 1950s»

AR5 WG1 Ch6 box 6.1 page 472 https://www.ipcc.ch/site/assets/uploads/2018/02/WG1AR5_Chapter06_FINAL.pdf 

Résumé pour les décideurs 5 en page 12 : Of these cumulative anthropogenic CO2 emissions, 240 [230 to 250] GtC have accumulated in the atmosphere. 

Munshi 2016   Corrélation émissions versus [CO₂].

[5]. La feuille de Calcul  Carbone 14 effet SUESS  met en forme les données d’observations.