English version here
also here
Nous venons d’apprendre que le prix Nobel de physique 2021 a été attribué ce mardi 5 octobre à deux experts de la modélisation du changement climatique, l’Américano-Japonais Syukuro Manabe et l’Allemand Klaus Hasselmann, ainsi qu’au théoricien italien Giorgio Parisi.
Le prix récompense pour moitié Syukuro Manabe, 90 ans, et Klaus Hasselmann, 89 ans, « pour la modélisation physique du climat de la Terre et pour en avoir quantifié la variabilité et prédit de façon fiable le réchauffement climatique« , précise le jury. L’autre moitié revient à Giorgio Parisi, 73 ans, « pour la découverte de l’interaction du désordre et des fluctuations dans les systèmes physiques de l’échelle atomique à planétaire ».
SCE félicite les lauréats et en profite pour rappeler quelques évidences que la plupart des médias se garderont bien de mentionner.
1. Le comité Nobel récompense des modélisateurs
Le prix Nobel de physique récompense des physiciens modélisateurs, c’est-à-dire des scientifiques qui utilisent des lois physiques bien connues pour élaborer des modèles mathématiques complexes, afin d’essayer de reproduire les évolutions passées et futures du système climatique.
Rappelons ici qu’un modèle mathématique n’est pas la réalité et qu’en ce qui concerne le climat, aucun modèle ne pourra jamais prédire ce qui se passera exactement dans le futur.
Voici pourquoi. Tout d’abord, nous ne connaissons pas encore de nombreux phénomènes physico-chimiques (exemple la formation des nuages). Si c’était le cas, la recherche scientifique pourrait s’arrêter aujourd’hui. Ensuite, le climat est un système complexe, c’est-à-dire qu’il est composé d’un grand nombre d’éléments (aussi bien sur Terre qu’en dehors de la Terre), et que tous ces éléments peuvent avoir entre eux un grand nombre d’interactions (Figure 1). De nombreux types d’interactions sont possibles; le système contient également de nombreuses boucles de rétroaction directes ou indirectes (et donc présentant un certain retard). Il est aussi dynamique, c’est-à-dire qu’il évolue dans l’espace et dans le temps.
Si les interactions entre les objets du système sont linéaires et instantanées, l’évolution du système dynamique en fonction du temps peut être modélisée par des systèmes d’équations différentielles ordinaires. Le système évolue alors au cours du temps vers une solution unique, où les valeurs des variables ne changent plus. On peut donc faire des prédictions.
Malheureusement les systèmes naturels possédant une propriété de linéarité sont rarissimes, pour ne pas dire inexistants. Cependant, de nombreux systèmes peuvent être raisonnablement linéarisés, afin de faciliter leur étude. C’est-à-dire qu’on peut les considérer, en première approximation, comme linéaires. De nombreuses théories relevant de la physique et de la mécanique sont ainsi construites en considérant des systèmes linéarisés.
Mais si les interactions entre objets du système sont non-linéaires (Rem : non-linéaire = le « principe de superposition » n’est pas respecté; la plupart des systèmes physiques sont non linéaires. Exemple : Équations de Navier-Stokes en mécanique des fluides) l’évolution du système dynamique en fonction du temps doit être modélisée par des systèmes d’équations différentielles non-linéaires. Ces équations sont très difficile à résoudre… Pendant très longtemps, on a dû recourir à des simplifications pour étudier ces équations dans des conditions de linéarité. Heureusement, les ordinateurs peuvent nous aider. Et ces ordinateurs nous montrent alors qu’il y a plusieurs solutions possibles! Dans certains cas, le système ne converge jamais directement vers l’une ou l’autre solution, mais « tourne autour » en orbites asymptotiquement convergentes; dans d’autres cas encore, le système évolue selon des orbites variables mais non convergentes autour d’un des « attracteurs étranges » et bascule à des moments imprédictibles d’un « attracteur » vers l’autre. Un tel système est dit « chaotique » (au sens mathématique du terme; « dynamical system » en anglais). Il peut se décrire par un système d’équations non linéaires parfaitement définies, mais la valeur de ses variables dépendantes à un moment donné peut changer énormément si l’on change de façon infime les conditions initiales ou la valeur d’un des paramètres, ce qui, en pratique rend un tel système parfaitement imprédictible. C’est ce que l’on a appelé le chaos déterministe. Le système oscille de façon irrégulière (apériodique) et ne reprends jamais deux fois exactement la même oscillation. Il ne sera alors pas possible de prévoir, à long terme, le comportement du système.
Dans le chaos déterministe, chaque condition initiale détermine entièrement l’évolution future car il n’y a pas de hasard : le système est déterministe. Cependant, deux conditions initiales très proches peuvent avoir des évolutions complètement différentes. L’évolution du système devient alors imprévisible car une petite erreur de mesure ou un arrondi à la 15ème décimale conduisent à des résultats complètement faux au bout d’un certain temps.
En d’autres mots, il suffit de changer légèrement une variable pour qu’un modèle climatique ne donne pas la même solution dans ses prévisions. Voici un exemple précis (Figure 2).
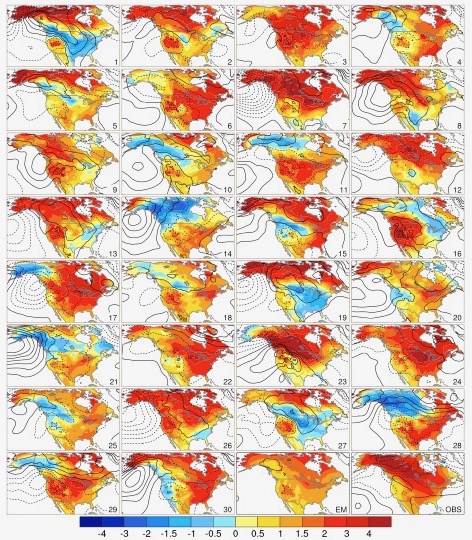
La Figure 2 (provenant de Deser et al. 2016, Journal of Climate 29:2237-2258) nous démontre que lorsque l’on fait varier la température de départ d’une valeur infinitésimale (10–14 °C), des prévisions complètement différentes peuvent être obtenues.
La moyenne des simulations (EM sur la Figure 2) n’est pas en accord avec les mesures observées, et pire, on fait dire aux modèles exactement ce que l’on veut, en modifiant un des paramètres de façon infinitésimale. On peut espérer naïvement que les modèles mathématiques (et leurs algorithmes calculant une moyenne) permettent de « gommer » la signature chaotique affectant un phénomène complexe, mais en réalité, les modèles eux-mêmes, par la structure des équations utilisées, donnent un caractère chaotique aux résultats qu’ils produisent.
Pour plus de détails, rappelons que SCE a publié ceci concernant les systèmes chaotiques.
2. Les modèles climatiques sont imprécis
Après ce qui vient d’être dit, il est évident que jury du Comité Nobel se trompe lorsqu’il écrit que les modèles climatiques peuvent prédire « de façon fiable le réchauffement climatique« . Voici encore deux observations qui montrent le contraire :
– Aucun modèle informatique n’avait prévu la pause (le « hiatus ») dans l’évolution des températures globales observé entre 1998 et 2014. Des dizaines d’articles ont été publiés sur ce problème. Voyez par exemple Hedemann et al. 2017 (Nature Climate Change).
– Les modèles informatiques, basés sur le taux de CO2, prévoient un « Hot-Spot » atmosphérique (nous vous en avions parlé ici). Cependant, ce « Hot Spot » ne correspond pas aux mesures réalisées in situ avec des ballons sondes ! Pour plus de détails voir Christy et al. 2018.
Pensez-vous toujours que les modèles climatiques sont précis? On sait depuis longtemps que les modèles climatiques présentent des taux de réchauffement excessifs dans la troposphère tropicale. Et ce n’est pas un secret pour de nombreux modélisateurs qui essayent d’améliorer leurs modèles… Il n’y a que le Comité Nobel qui n’a pas l’air au courant!
Concernant les nouvelles versions des modèles climatiques CMIP6 (Coupled Model Intercomparison Project Version 6), utilisées dans le dernier rapport du GIEC (AR6), elles ne sont pas meilleures. Par exemple, dans une publication de 2020, McKitrick et Christy ont examiné 38 modèles CMIP6 en utilisant des paramètres historiquement observés. Ils se sont concentrés sur l’intervalle 1979-2014. Les auteurs montrent que les modèles produisent des réchauffement qui ne correspondent pas avec les observations que cela soit pour la basse ou la moyenne troposphère, au niveau des tropiques ou ailleurs dans le monde.
3. La philosophie du prix Nobel n’est peut-être pas respectée
Il n’est pas certain qu’Alfred Nobel ait approuvé le prix de physique 2021 au cas où il aurait pu en prendre connaissance. Inventeur de la dynamite, il était passionné par les aspects concrets de la science et de la technologie et avait à cœur de récompenser celles et ceux qui avaient contribué de manière tangible à leurs progrès. Ainsi, le prix Nobel de physique de 1903 fut attribué conjointement aux époux Curie (Pierre et Marie) et à Henri Becquerel pour leur découverte de la radioactivité naturelle, phénomène physique inconnu à l’époque. Celui de 1935 fut attribué à James Chadwick pour récompenser sa découverte du neutron en 1932, un élément essentiel, constitutif de la matière. Les exemples de ce type abondent.
Ce n’est que progressivement que le prix fut également attribué à des théories de nature plus ésotérique. Une des conditions de l’attribution était l’éclairage que ces théories pouvaient fournir à la compréhension des propriétés du monde physique. Un excellent exemple est le prix Nobel de physique 1963, attribué Eugène Wigner (conjointement avec Maria Goeppert-Mayer et Hans Jensen) pour des travaux fondamentaux consacrés aux groupes de symétrie, une théorie mathématique très abstraite permettant de comprendre d’importants aspects de la structure de l’univers.
Plus près de nous, le Nobel de physique de 2013 récompensa deux théoriciens (Brout et Englert) à l’origine d’un modèle mathématique justifiant les propriétés d’une particule fondamentale, le boson de Higgs, mise en évidence en 2012 dans les instruments de détection autour du grand collisionneur du CERN. Cette mise en évidence explique l’attribution du prix aux trois auteurs dont deux seulement en bénéficièrent, Brout étant décédé en 2011.
Le prix de cette année est loin de s’inscrire dans cette perspective. Les auteurs du modèle récompensé amènent-ils des résultats inédits ? On peut en douter, à l’exception peut-être de Giorgio Parisi. L’attribution se contente de mentionner des résultats ‘fiables’. Le moins que l’on puisse dire est que ce qualificatif ne signifie pas grand-chose. Par ailleurs, le modèle ne fournit rien de fondamentalement nouveau en matière de physique. Tout ce qui le constitue (physique du soleil, de l’atmosphère, des océans et leurs interactions) est connu depuis des décennies. Le prix va donc à un exercice plus ‘mathématique’ que ‘physique’. La volonté d’Alfred Nobel est donc en quelque sorte trahie.
4. Conclusions
En récompensant des modélisateurs du climat à la veille de la COP26, le Comité Nobel fait un geste politique et médiatique. Le commun des mortels, qui ne connaît rien aux modélisations, aura ainsi tendance à croire ce qui est prédit dans le Saint Rapport du GIEC.
Pour terminer, rappelons ici ce qu’avait écrit physicien Jacques Duran sur son site « Pensée-unique » :
« Les prévisions sur le futur de notre planète sont pour le moins hasardeuses car nous avons affaire à un énorme système d’équations différentielles à coefficients inconnus, non linéaires et couplées entre elles. Ces équations sont donc très difficiles à élucider. En plus, certaines de ces équations se comportent de manière chaotique, c’est-à-dire qu’elles sont très sensibles aux conditions initiales souvent inconnues. Il n’y a pas pire ! Pourtant, les programmeurs sur ordinateurs s’en donnent à cœur joie avec des milliers de paramètres inconnus et la forme des équations maîtresses qu’il faut essayer de deviner. Disons gentiment que, comme toujours, ils obtiennent des résultats mais le problème c’est que l’on peut faire évoluer les résultats comme on le désire en changeant un seul des paramètres ou une seule des équations inconnues. Comment croire alors que les ordinateurs font une prédiction correcte alors que les mécanismes essentiels des échanges et des rétroactions (feedbacks) positives et négatives sont encore très mal comprises et font toujours l’objet d’âpres discussions entre les chimistes, physiciens, climatologues, et géophysiciens? »
« La croyance dans la véracité de telle ou telle prédiction d’ordinateur relève plus de la foi que de la certitude scientifique. Étant donné la multiplicité des méthodes de résolution possibles, les équations hasardeuses et le nombre de paramètres injectables, les résultats des simulations sur ordinateur sont très difficilement contrôlables par quiconque ne les a pas programmées lui-même. Bref, on nage dans le flou et les partis-pris prennent le dessus. Pour leur part, les politiques et les écologistes choisissent les résultats qui leurs conviennent, mais ils ignorent tout des nombreuses incertitudes, des approximations et des problèmes que posent les méthodes qui ont été employées. Les politiques et les écologistes sont dans l’incapacité totale d’apprécier la fiabilité des résultats qui leur sont communiqués et l’on ne saurait leur en vouloir au vu des difficultés du problème. La seule chose que l’on peut leur reprocher c’est leur trop grande crédulité et leurs affirmations péremptoires pour faire croire que tout cela est sûr et certain. Alors que ça ne l’est pas du tout! »
4. Références
John R. Christy, Roy W. Spencer, William D. Braswell & Robert Junod (2018) Examination of space-based bulk atmospheric temperatures used in climate research, International Journal of Remote Sensing, 39:11, 3580-3607, DOI: 10.1080/01431161.2018.1444293.
pour en savoir plus : lisez ceci.
Laisser un commentaire