Roland Van den Broek, Ingénieur civil
Henri Masson, Professeur (émérite) à l’Université Antwerpen
Avant-propos
Ce document est la synthèse d’une étude beaucoup plus détaillée qui est en cours de finalisation et sera publiée en format PDF dans quelques semaines. Les lecteurs qui ne seraient pas rassasiés par cette mise en bouche pourront s’y référer pour approfondir le sujet.
Cette étude décrit un modèle thermique très simple qui permet d’expliquer toutes les observations des températures océaniques depuis 1850 jusqu’à nos jours en se basant sur l’activité solaire et un terme harmonique.
Cette étude montre que la température océanique annuelle moyennée par latitude est le reflet du rayonnement solaire annuel incident par latitude. Il en résulte que bien qu’étant une grandeur intensive qui n’a en principe qu’une signification thermodynamique locale, la température locale peut être moyennée spatialement pour en dériver une température ou une anomalie de température globale.
L’étude décrit également un autre modèle, basé sur la loi de Henry et la relation de van ‘t Hoff, qui révèle que la concentration naturelle en CO2 atmosphérique, estimée selon trois approches différentes, dépend de la température. La relation trouvée entre la température et la concentration naturelle en CO2 atmosphérique est analogue à la formule semi-expérimentale de Myhre qui reçoit ainsi une justification théorique non basée sur un effet radiatif du CO2, et qui est utilisée en sens contraire par le GIEC. L’accord entre la théorie et les observations est excellent lorsqu’on utilise une constante de temps de résidence du CO2 d’environ 15 ans, qui correspond précisément à celle qui a été observée après l’arrêt des essais thermonucléaires atmosphériques au début des années 1960.
Ces modèles ont été validés par des tests de causalité statistique, et des analyses de corrélation croisée montrent que le signal de la température contient la signature de l’activité solaire.
Ces analyses sont tout à fait à l’opposé des thèses du GIEC. Elles permettent de considérer que le climat évolue de manière entièrement naturelle sous la seule influence de l’activité solaire combinée à un effet intégrateur des océans, qui peut amplifier, avec un certain retard l’effet de faibles variations d’irradiance solaire, pour peu qu’elles perdurent assez longtemps.
1. Soleil et température
Le GIEC utilise un modèle statique du climat qui peut se résumer comme suit:
- le climat se serait stabilisé avant l’époque pré-industrielle.
- le rayonnement solaire n’a quasiment pas changé depuis lors.
- la couverture nuageuse reste constante.
- l’augmentation du taux de CO2 atmosphérique est exclusivement d’origine anthropique et découle uniquement de l’usage de combustibles fossiles.
- cette contribution anthropique aux émissions de CO2 est discernable des contributions naturelles, en utilisant la signature isotopique comme marqueur.
- cette augmentation du CO2 est la seule cause de l’augmentation de la température par le biais d’un « effet de serre atmosphérique » radiatif.
- les contributions naturelles (nuages, aérosols, etc.) sont considérées comme des “forcings”, que l’on peut associer mathématiquement à des rétroactions positives ou négatives, qui respectivement amplifient ou amortissent “l’effet de serre atmosphérique”.
- dans ses modèles dits de circulation globale, le système climatique est localement à l’équilibre et les transferts de matière et chaleur entre cellules locales sont définis par les équations de Navier-Stokes.
Le GIEC ignore complètement la variation climatique liée aux variations d’intensité du rayonnement solaire, un phénomène qui a toujours existé, et ne cherche qu’à prouver, conformément à ses statuts et à son mandat, que l’activité humaine est la seule cause du réchauffement climatique.
Avec ces hypothèses qui heurtent le bon sens, le GIEC ne peut que faire sienne la citation de Confucius : « Vous ne trouverez pas ce que vous ne cherchez pas ». Le soleil est la première source d’énergie de notre planète et est la cause des variations de température que nous observons, qu’elles soient journalières, annuelles ou sur de plus longues périodes. A toutes les échelles de temps, l’activité solaire varie et a un impact majeur sur la température terrestre.
L’examen de l’activité solaire montre qu’elle a augmenté au cours du siècle précédent et est passée par un maximum à la fin de ce dernier. Ceci pourrait expliquer l’augmentation des températures observées, mais la diminution récente de l’activité solaire n’a pas produit une diminution sensible de la température, ce qui est un argument utilisé par le GIEC pour conforter sa position.
Comment expliquer cette contradiction ?
Il est venu à l’idée de prendre en compte la moyenne de l’activité solaire sur un certain nombre d’années plutôt que sa valeur instantanée. Ceci introduit un tampon qui a un rôle d’amortisseur thermique joué par les océans. Ceux-ci couvrant 70 % de la surface de la planète et ayant une capacité de stockage de la chaleur qui est de quelques ordres de grandeur supérieure à celle de l’atmosphère, il a été décidé de limiter les analyses aux températures océaniques. Ces dernières présentent également l’avantage de ne pas être contaminées par des effets d’îlot urbain de chaleur.
Cette idée s’est avérée très fructueuse. En la combinant avec un terme harmonique, on obtient une recette de calcul qui permet de reproduire très fidèlement les températures observées. Voir Fig. 1.
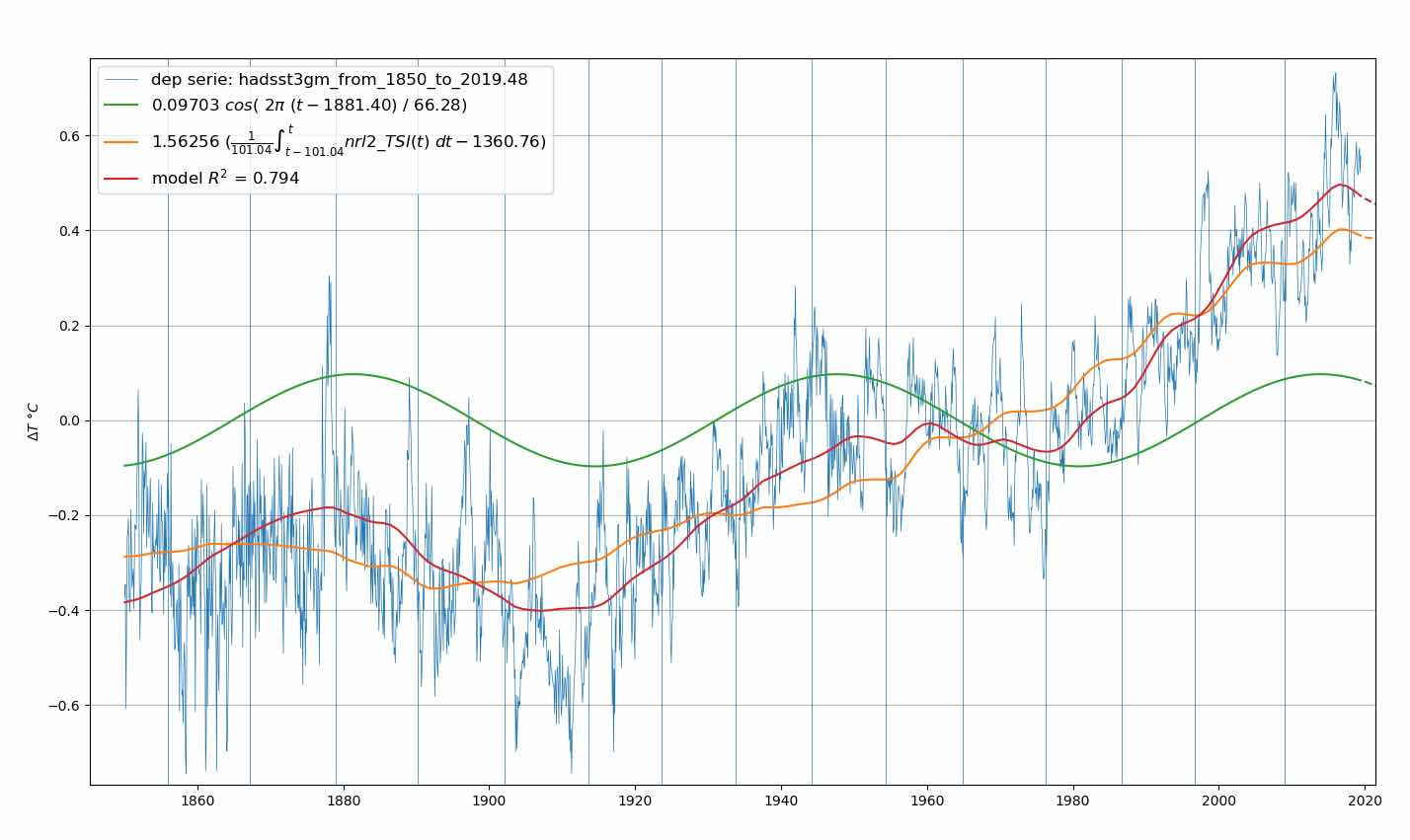
En vert, le terme harmonique avec une amplitude d’environ un dixième de degré et une période d’environ 66 ans.
En orange, le terme correspondant à la moyenne mobile sur environ 100 ans du rayonnement solaire (NRL2_TSI, yearly averages). En rouge, le modèle (somme des 2 termes précédents). En bleu, les températures océaniques (HadSST3). Tous les paramètres ont été optimisés par analyse de régression non linéaire. Le terme basé sur le rayonnement solaire moyen et le terme harmonique viennent de passer par un maximum et commencent à diminuer maintenant
Mais c’est bien plus qu’une recette. Des investigations complémentaires ont révélé que c’est une solution approchée de l’équation différentielle d’un modèle thermique simple qui régit l’évolution de la température de surface océanique en fonction du rayonnement solaire.
Voir annexe 4.1.1.
La corrélation croisée des séries de température et du rayonnement indique que l’évolution de la température suit celle du rayonnement solaire avec un décalage égal au quart de la période moyenne des cycles solaires qui vaut environ 11 ans. Ce décalage est en accord avec la solution de l’équation différentielle du modèle thermique dans le cas d’une stimulation périodique. Le signal de la température contient donc la signature de l’activité solaire.
La reconstruction de l’irradiance solaire qui a été utilisée dans les analyses, remonte jusqu’en 1610 et permet d’estimer les températures à partir de 1715. Cette estimation montre une sortie vraisemblable du petit âge glaciaire dans laquelle on retrouve les minimums de Maunder et de Dalton. Voir Fig. 2.
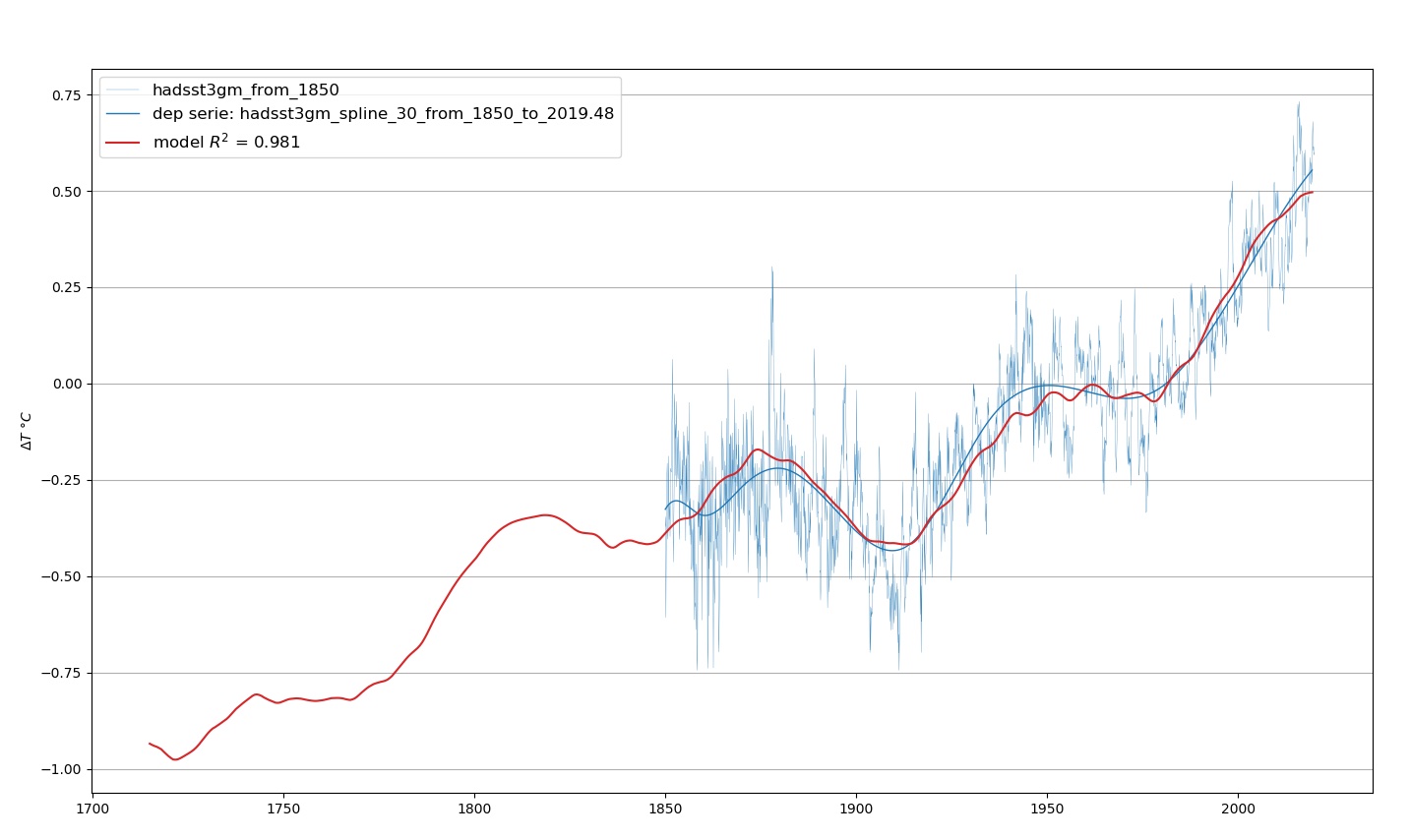
On retrouve le minimum de Maunder entre 1700 et 1750, ainsi que le minimum de Dalton entre 1800 et 1850.
Dans cet exemple, les températures océaniques ont fait l’objet d’un lissage par spline pour neutraliser les phénomènes El Niño – La Niña. Ceci débouche sur une corrélation impressionnante.
L’activité solaire est à la baisse depuis quelque temps. Le dernier cycle solaire était très faible, et celui qui est en cours semble marcher dans ses traces. Si cette tendance se confirme, nous pourrions observer dans les prochaines décennies une diminution des températures à peu près symétrique de l’augmentation observée au cours du dernier siècle. Il en résulterait que les objectifs des Accords de Paris 2015 seraient atteints naturellement, en l’absence de tout plan de transition énergétique.
Une analyse de la série de températures hadisst du Met Office – Hadley Centre montre qu’à chaque latitude, les moyennes annuelles des températures de surface océaniques sont très bien modélisées par la moyenne annuelle du rayonnement solaire incident. Voir Fig. 3. Ceci s’explique également par le modèle thermique sous-jacent. Voir annexe 4.1.2.
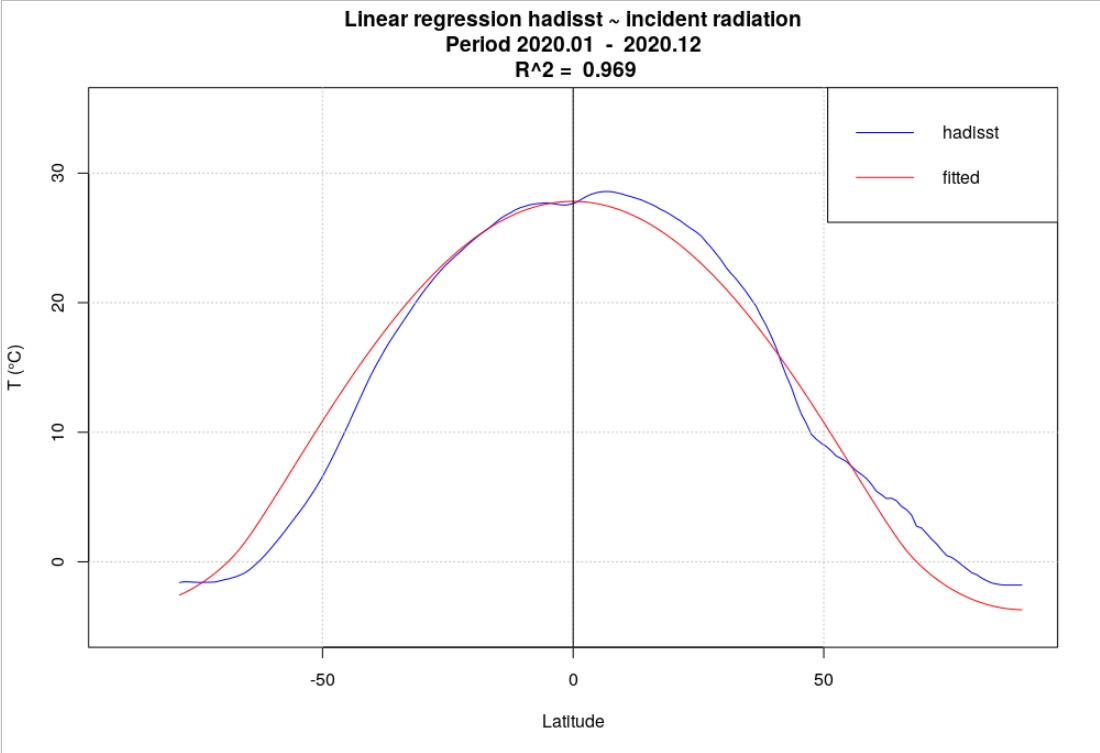
Finalement, des analyses de causalité statistique au sens de Granger révèlent que le rayonnement solaire moyen est la cause de la température, et que le rayonnement solaire non moyenné ne l’est pas.
Avec un faisceau de présomptions aussi fortes, comment pourrait-on encore douter du rôle moteur du Soleil dans le mécanisme climatique ?
2. Température et CO2
Dans sa modélisation du cycle du CO2, le GIEC considère que les émissions naturelles de CO2 sont rapidement absorbées et que les émissions anthropiques demeurent très longtemps dans l’atmosphère. Cette hypothèse est en contradiction avec le Principe d’indiscernabilité ; quelle que soit l’abondance isotopique dans un flux de CO2 donné, les molécules se comportent de la même façon, macroscopiquement, d’un point de vue thermodynamique et physico-chimique. C’est par ailleurs la propriété caractéristique qui justifie l’utilisation de marqueurs radioactifs dans un large spectre d’utilisations.
Par quelques considérations de chimie-physique et de physique élémentaires basées sur la loi de Henry et la relation de van’t Hoff, on retrouve assez facilement la formule semi-expérimentale de Myrhe utilisée par le GIEC qui lie le forcing radiatif et la température à la teneur en CO2. Voir annexe 4.2. On peut donc interpréter la formule de Myhre comme une conséquence de la loi de Henry plutôt que d’un « effet de serre atmosphérique » radiatif qui, contrairement à la loi de Henry, n’a jamais été prouvé expérimentalement dans les basses couches de l’atmosphère.
Certains argueront que la loi de Henry ne peut justifier qu’une faible part de l’augmentation de la pCO2 observée depuis l’époque préindustrielle, mais un calculateur en ligne de la chimie carbonatée de l’eau de mer, publié par l’Université du Colorado prouve que ce n’est pas le cas. En utilisant ce calculateur, on remarque que la pCO2 est égale à 263.5 ppm dans le scénario Preindustrial et passe à 380.7 ppm dans le scénario Modern, alors que la différence de température entre ces deux scénarios n’est que de 1.6 °C. En plus de la température, ce calculateur utilise 2 autres paramètres (l’alcalinité (TA) et le carbone inorganique dissous (DIC)) qui ont un impact important sur la pCO2.
En faisant varier linéairement tous les paramètres entre leurs valeurs respectives des scénarios Preindustrial et Modern, une analyse de régression aboutit à la même liaison entre le log(CO2) et la température que la loi de Henry.
La relation trouvée est la suivante :
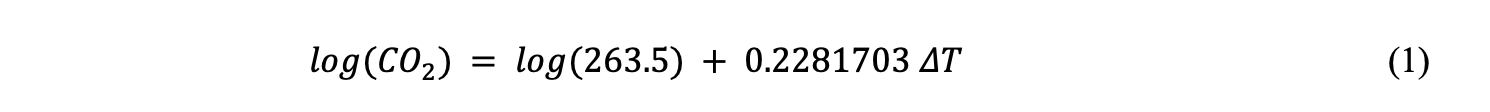
En première approximation , l’équilibre entre les teneurs en CO2 océanique et atmosphérique est analogue à un système de deux vases communicants dont le niveau d’équilibre ne peut être changé que par la température. Le premier vase correspond aux océans, et le second à l’atmosphère. Les océans contiennent environ 50 fois plus de CO2 que l’atmosphère.
La formule (1) permet de calculer la variation de CO2 pour une variation de température donnée.
L’équilibre de Henry est bidirectionnel. Ceci est confirmé par des analyses de causalité au sens de Granger. Cette formule peut donc également être lue en sens inverse pour calculer la variation de température suite à une variation de CO2.
Sur base du cycle du carbone d’après le GIEC (AR5 WG1 Chapitre 6), on peut évaluer à 0.045°C l’augmentation de température due au cumul des émissions anthropiques depuis l’ère préindustrielle, lorsque l’équilibre des pCO2 océanique et atmosphérique sera atteint.
Suivant le même principe, on peut calculer l’augmentation de température pour un doublement de la pCO2. On obtient ∆T = log(2)/0.228 = 3.04°C. Cette valeur est importante, mais est complètement irréaliste, parce que pour doubler la pCO2 , il faut doubler la quantité de carbone atmosphérique ET la quantité de carbone océanique qui est environ 50 fois plus importante. Pour la même raison, la capture et le stockage du carbone est une ineptie. Si on retirait de l’atmosphère le total cumulé du carbone anthropique émis jusqu’à ce jour, on n’obtiendrait qu’une diminution de température de 0.045 °C.
L’équilibre de Henry – van ‘t Hoff n’est pas instantané. L’arrêt des essais atmosphériques de bombes thermonucléaires au début des années 1960 montre une décroissance exponentielle du 14C libéré par les explosions, avec une constante de temps d’environ 15 ans. Certains auteurs estiment que cette valeur pourrait être plus faible par suite d’effets de réémissions.
Dans l’hypothèse d’un mélangeur parfait à simple flux, le CO2 naturel a été calculé en déduisant du CO2 relevé à Mauna Loa les émissions anthropiques en supposant une constante de temps de résidence de 15 ans. Une analyse de régression avec la température océanique hadsst3 fournit la relation suivante :
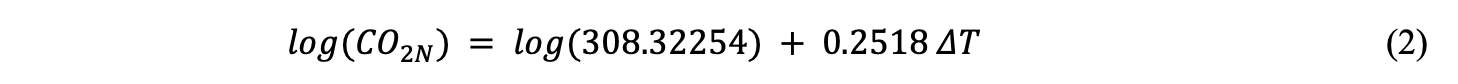
Avec un modèle plus sophistiqué à double flux et la série de température GISS, tel que décrit dans Harde 2019, on obtient un résultat analogue :
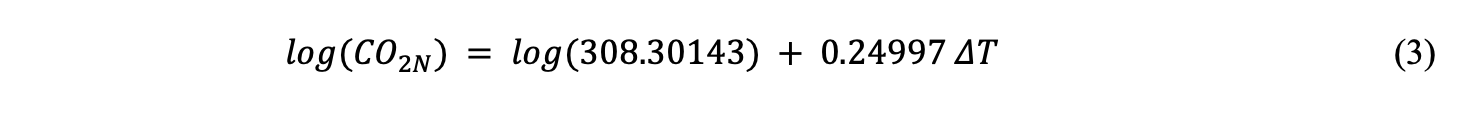
Ces trois formulations sont très voisines et confortent l’hypothèse que l’équilibre de Henry – van ‘t Hoff est à l’oeuvre dans les variations de température et du CO2.
La part anthropique du CO2 atmosphérique dépend fortement de la constante de temps de résidence et doit respecter certaines contraintes d’abondances isotopiques sur le Δ14C lié à l’effet Suess et le δ13C qui dépend de l’usage de combustibles fossiles. Dans les modèles à simple et double flux, différentes valeurs de la constante de temps de résidence ont été prises en considération, et c’est la valeur de 15 ans qui respecte le mieux ces contraintes.
3. Conclusions
C’est le soleil qui règle le climat. La concentration en CO2 est un effet de la température (et des émissions anthropiques) au lieu d’en être la cause.
Un modèle simple permet d’expliquer les températures observées depuis 1850 jusqu’à maintenant sur la seule base du rayonnement solaire, avec un éventuel terme harmonique complémentaire, sans devoir recourir à un hypothétique effet de serre radiatif du CO2.
Une formule simple, analogue à celle de Myhre, montre que la concentration en CO2 atmosphérique naturel dépend de l’anomalie de température globale. Cette même formule est lue dans le mauvais sens par le GIEC qui confond cause et effet.
Il a suffi de trente années de manipulations politiques pour pousser les sciences climatiques dans la mauvaise direction et les amener dans une situation digne du Moyen-Age. En dépit d’hypothèses qui heurtent le bon sens, le GIEC a réussi à ranger de son côté les médias, une grande partie du monde politique et de trop nombreuses Académies des Sciences, en faisant simplement valoir l’argument d’un prétendu consensus, ce qui est contraire à toute démarche scientifique.
Dans un futur pas très lointain, le Soleil va vraisemblablement montrer qu’il est le principal maître à bord en matière de climat. Aucun modèle mathématique ne sera nécessaire pour le comprendre. Le naufrage de nos démocraties, manipulées par un agenda politique pseudo-scientifique, est en cours. Il est préférable de ne pas attendre pour prendre conscience que nos sociétés sont en train de déraper et de s’interroger dès aujourd’hui sur les causes de ce dysfonctionnement.
Se croyant dans un monde imaginaire où 2 et 2 pourraient faire 5, les signataires des Accords de Paris ont décidé que nous devons nous lancer dans des plans de transition énergétique qui auront un coût financier astronomique sans aucun impact discernable sur le climat.
L’impact sur le PIB, résultant de la fermeture ou délocalisation d’industries dites polluantes car générant des quantités importantes de CO2, serait énorme pour ne pas dire suicidaire. Il en va de même sur le plan social, vu le nombre de personnes qui perdraient leur emploi. Sans parler des finances publiques, déjà exsangues dans de nombreux pays, et qui seraient sollicitées au-delà du supportable, à coups de subsides, allocations, avantages fiscaux et autres mécanismes de marché.
Tenter de compenser ces dépenses par des taxes carbone se répercuterait en fin de compte sur le coût de la vie, induisant une inflation galopante et une précarité énergétique accrue. Tous les ingrédients sont réunis pour engendrer des mouvements sociaux, comme celui des gilets jaunes.
L’objectif du GIEC est de limiter l’exploitation des ressources terrestres et d’imposer un agenda politique non démocratiquement choisi sous le prétexte d’une soi-disant urgence climatique qui dépasse les souverainetés nationales. (Voir ici, ici, ici, ici, ici et ici ). Ses représentants ne s’en cachent d’ailleurs pas (Voir ici). Malheureusement, les politiques climatiques préconisées provoqueront un appauvrissement généralisé (Voir ici), et il vaudrait bien mieux allouer à des mesures de nivellement par le haut, les montants inconsidérés qu’elles requièrent.
Il est urgent de sauver la planète, non pas du climat, mais de ceux qui ont perdu tout bon sens et tout esprit critique. Ils sont prêts à mettre en œuvre leurs plans complètement irrationnels. Il faut réagir dès maintenant. Une entreprise de Bill Gates veut pulvériser de la poussière dans l’atmosphère pour diminuer le rayonnement solaire. Faut-il vraiment refroidir la planète alors que nous sommes vraisemblablement en route vers un nouveau petit âge glaciaire ? Dans les années 1970, on s’inquiétait de la diminution des températures depuis 1945, et des “experts” mal informés ont suggéré de répandre de la suie sur les Pôles pour réchauffer la Terre en diminuant son albédo.
Avec des médias complètement hermétiques au climato-réalisme, il ne reste que le bouche-à-oreille qui peut néanmoins être très efficace dans sa version moderne. Tous les arguments sont là pour remettre à sa place n’importe quel alarmiste climatique.
Les médecins ont continué à pratiquer les saignées pendant 200 ans après qu’il ait été prouvé que cela n’avait aucun sens. La situation peut se normaliser plus rapidement à condition de ne pas garder la vérité pour soi. Si vous voulez quitter le Moyen-Age dans lequel vous avez été replongés, et préférez vivre dans un monde débarrassé de discours climatiques anxiogènes infondés, diffusez ce message en masse sans plus tarder. Les générations futures vous en remercieront.
4. Annexes mathématiques
4.1 Modèle thermique
4.1.1 Rayonnement solaire et température globale
Il est intéressant de noter que la modélisation de l’anomalie de température par une moyenne du rayonnement solaire n’est qu’une autre formulation d’un modèle thermique utilisé dans Stockwell (2011) [1]:


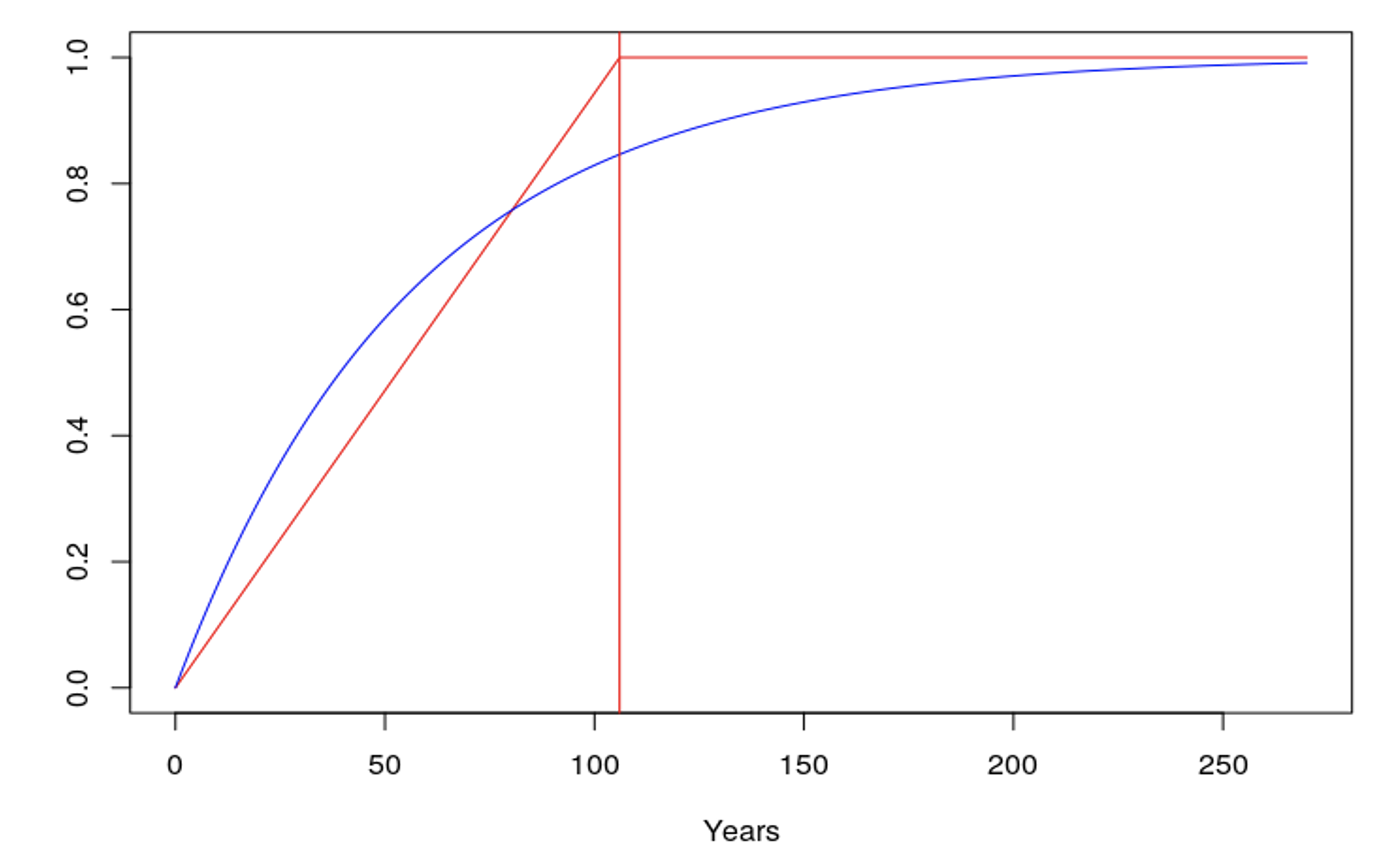
Dans cet exemple T = 106ansekt = 56,6ans.. La valeur de k a été déduite de


4.1.2 Rayonnement solaire et température globale
L’examen de la série de température hadisst révèle qu’à une latitude donnée, les températures de surface océaniques varient peu à latitude constante, et qu’en moyenne annuelle, en formalisant l’analyse de régression (Fig. 3), on a :


Moyennant un choix adéquat de sa température de référence, l’anomalie globale de température annuelle moyenne est proportionnelle au rayonnement incident annuel moyen.
Bien que la température de surface océanique soit une grandeur intensive, il est tout à fait légitime d’en faire des moyennes spatiales pour calculer une anomalie globale, parce qu’en procédant ainsi, on ne fait que moyenner des rayonnements, ce qui est tout à fait correct. C’est la relation (18) qui justifie cette pratique.


4.2 Formule de Myhre, loi de Henry et relation de van ‘t Hoff
Le GIEC utilise une formule semi-empirique pour lier le forcing radiatif à la teneur en CO2.
Cette formule provient d’un article de G. Myrhe et al. (1998)[3] :
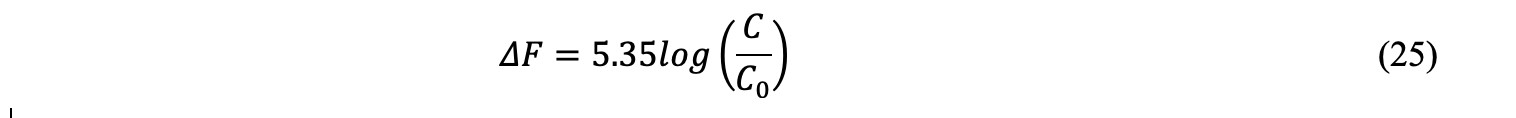

C’est sur cette base que le GIEC prétend que les émissions anthropiques de CO2 provoquent une augmentation du taux de CO2 atmosphérique qui conduit à une augmentation du forcing radiatif qui fait augmenter la température. Mais remarquons au passage que cette expression empirique ne donne pas la direction du lien de cause à effet. Quelques considérations de chimie-physique et de physique élémentaires permettent d’éclaircir cette question.
En recourant à la loi de Henry qui décrit l’équilibre gaz-liquide, et à la relation de van ‘t Hoff qui tient compte de la température, on peut obtenir une formule théorique cette fois, qui est analogue à la formule (25).
La concentration océanique de CO2 est liée à la pression partielle du CO2 dans l’atmosphère par la loi de Henry



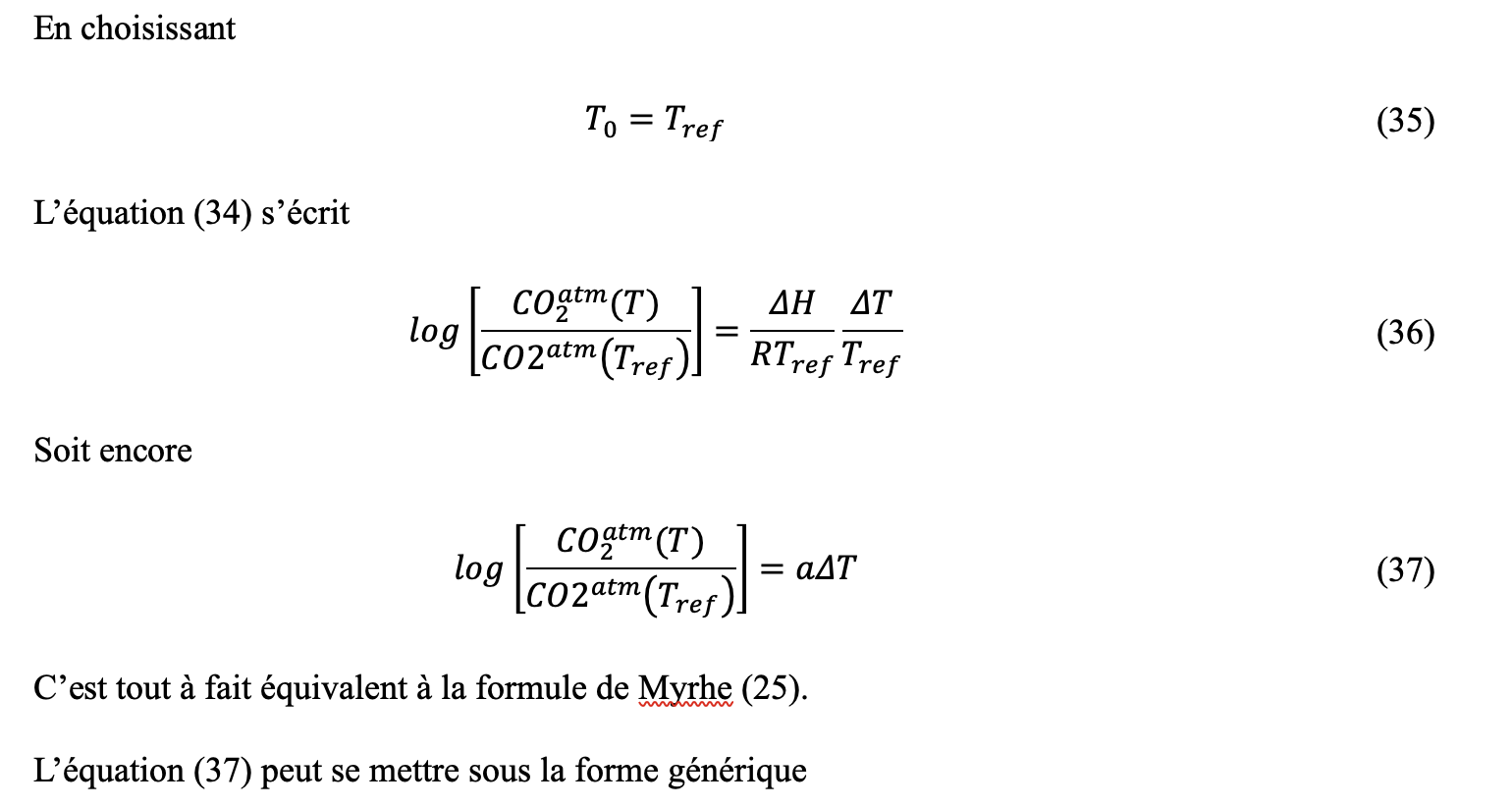
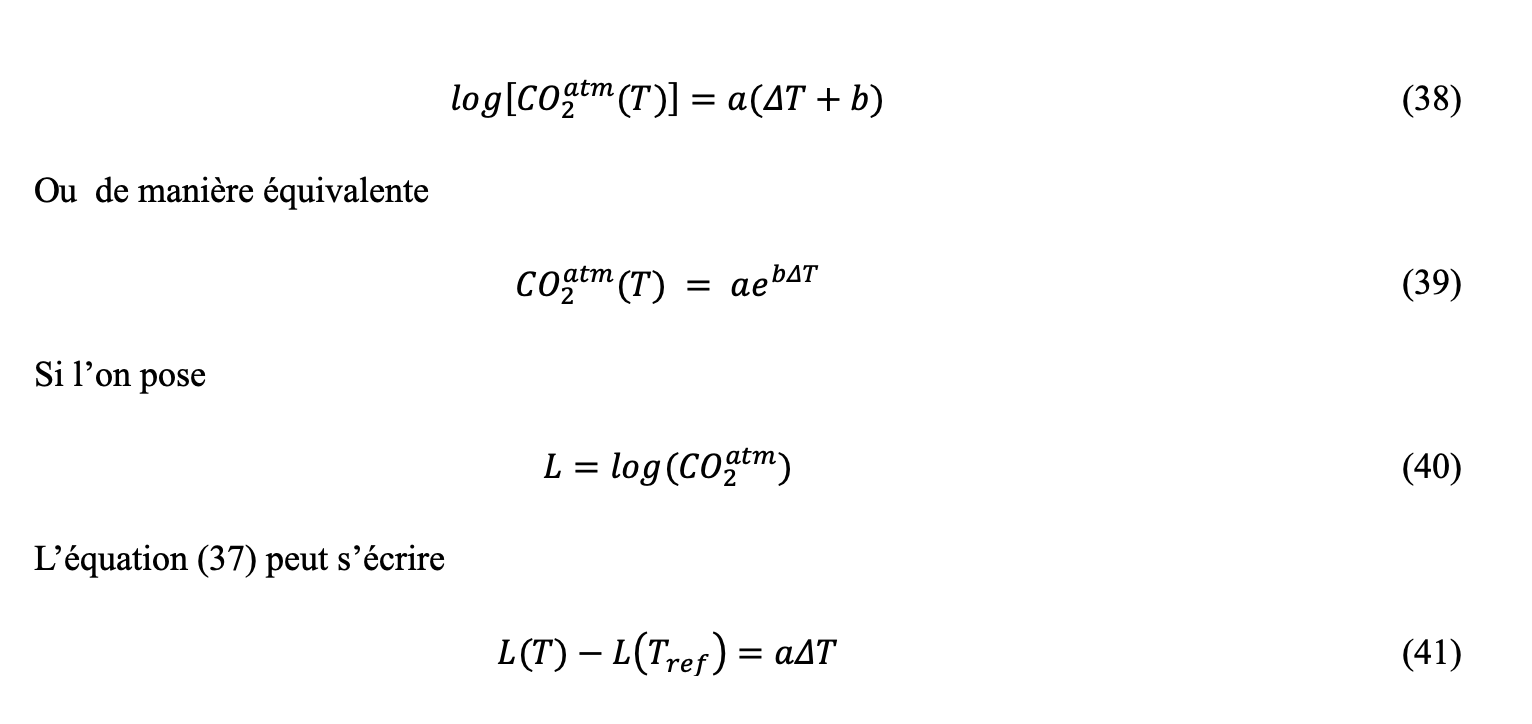
C’est l’équation de la dilatation linéaire. La variation du logarithme du taux de CO2 atmosphérique est analogue à la variation de longueur d’une barre soumise à une variation de température.
On peut également faire la comparaison suivante.
L’équilibre entre le CO2 océanique et le CO2 atmosphérique est analogue à un système de deux vases communicants dont l’équilibre des teneurs en CO2 dans chaque vase est régi par loi de Henry. Le premier de très grande surface contenant le CO2 océanique, et le second de surface beaucoup plus petite contenant le CO2 atmosphérique. Ajouter du CO2atmosphérique par des émissions anthropiques, ou en retirer par de la capture et stockage, dans le compartiment à faible surface n’aura pratiquement aucun effet sur le niveau, lorsqu’un nouvel équilibre sera établi. Il n’y a que la température qui puisse faire changer le niveau d’équilibre, de manière analogue à une dilatation/contraction thermique. C’est cette analogie qui prouve que la variable indépendante (causale) est ∆T et non pas le CO2, ce qui contredit l’interprétation de la formule de Myhre faite par le GIEC.
Le même raisonnement peut être tenu pour les autres gaz à « effet de serre » pour lesquels les conclusions précédentes sont également d’application.
NOTES
[1] Stockwell 2011 On the Dynamics of Global Temperature
[2] Mc Cabe, Smith & Harriott 1993 Unit Operations of Chemical Engineering, pg 422
[3] Myhre, Highwood, Shine & Stordal 1998. New estimates of radiative forcing due to well mixed greenhouse gases
L’article a cent fois raison. Il faut cesser de nous bassiner avec l’effet de serre.
L’effet de serre ne fait que réchauffer l’atmosphère, laquelle a une inertie thermique bien plus faible que les sols et infiniment plus faible que l’eau des couches supérieures des océans. L’effet de serre ne joue sur le réchauffement climatique de la planète que de façon marginale.
De plus le CO2 dont on nous rebat les oreilles est peut-être un gaz à effet de serre en laboratoire mais pas dans l’atmosphère où il est en mélange avec d’autres gaz, principalement la vapeur d’eau. Or H2O présente un spectre d’absorption des IR aux larges bandes qui recouvrent totalement (en fréquence et en intensité) celles du CO2. De ce fait et compte tenu de la quantité bien plus élevée dans l’atmosphère d’humidité que de CO2, c’est l’eau qui absorbe les infrarouges et la quantité restante absorbée par le CO2 est infime. C’est le phénomène physique dit de saturation qui fait que le CO2 atmosphérique ne peut être comptabilisé dans les GES. Le principal gaz à effet de serre est l’eau atmosphérique (à 80-90% + le méthane et l’ozone à quelques % chacun).
Voir par exemple:
http://co2climate.e-monsite.com/pages/la-definition-de-l-effet-de-serre-climatique-utilisee-par-le-giec-est-elle-valable.html
Ce que vous dites contredit le principe de conservation de la masse.
Un très simple bilan matière suffit à démonter cela.
La question est « Est ce tout l’excès de CO2 dans l’atmosphère vient des activités humaines ? ».
Pour mémoire cet excès est de 130 ppmv (410 – 280) et augmente de 2,5 ppmv par an actuellement. Les activités humaines (charbon, pétrole, gaz,..) émettent environ 40 Milliards de tonnes de CO2 par an actuellement.
Ramené à la masse de l’atmosphère de 5.1 Millions de Milliards de tonnes, cela fait 7.8 ppmm (massique). Multiplié par le ratio des masses molaires Air/CO2=29/44, cela fait 5 ppmv (volumique) de CO2 émis chaque année par les activités humaines vers l’atmosphère. Donc 2 fois plus que la hausse mesurée de 2,5 ppmv de la concentration de CO2. La différence est absorbée par la biosphère (végétation terrestre + océans). Donc la réponse est oui, tout l’excès de CO2 de l’atmosphère vient actuellement des activités humaines, et oui l’océan absorbe en net annuel du CO2 et n’en émet pas. Et il s’acidifie (même Claude Allègre disait cela, c’est dire !…)..
Monsieur,
Votre calcul est faux pour deux raisons.
D’une part, vous ne tenez pas compte des émissions totales (naturelles et anthropiques). Ceci vous a déjà été expliqué en long et en large dans un autre fil de discussion sur ce site. Nous n’y reviendrons pas.
D’autre part, vous ignorez complètement l’équilibre de Henry – van ‘t Hoff. La chimie carbonatée de l’eau de mer est assez compliquée et nécessite la résolution d’un système non linéaire de 6 équations à 6 inconnues. Heureusement un calculateur en ligne mis au point par l’Université du Colorado vient à la rescousse. Voir https://biocycle.atmos.colostate.edu/shiny/carbonate/ . Il montre que la pCO2 est passée de 263.5 ppm (scénario Preindustrial) à 380.7 ppm (scenario Modern) pour une augmentation de température de 1.6 °C. L’équilibre de Henry – van ‘t Hoff explique donc les 3/4 de la variation du CO2 observée à Mauna Loa. On est loin d’une origine exclusivement anthropique. Le quart restant s’explique par le fait que l’équilibre de Henry – van ‘t Hoff n’est pas instantané. Si la température devait se stabiliser et en l’absence d’émissions anthropiques complémentaires, les pCO2 de l’océan et de l’atmosphère finiraient par se stabiliser, par une décroissance exponentielle de l’excédent atmosphérique, avec une constante de temps de résidence que l’on peut estimer à 15 ans, telle qu’elle a été observée après l’arrêt des essais thermonucléaires au début des années 1960.
Le calculateur en ligne décrit un équilibre naturel des pCO2 océanique et atmosphérique indépendamment des émissions anthropiques. Ses équations satisfont non seulement au bilan de matière, mais aussi au bilan d’énergie à l’interface océan-atmosphère, ce dernier étant absent dans votre raisonnement.
Si vous pensez que ce n’est pas le cas, vous devriez expliquer aux spécialistes de la chimie carbonatée de l’eau de mer que leur calculateur est faux. Nous vous souhaitons bon courage
J’ai noté le passage où vous dites »La corrélation croisée des séries de température et du rayonnement indique que l’évolution de la température suit celle du rayonnement solaire avec un décalage égal au quart de la période moyenne des cycles solaires qui vaut environ 11 ans » Je ne suis pas certains qu’il s’agisse très exactement de la même chose mais on voit bien une relation avec déphasage de 1/4 de période entre les cycles solaires de 11 ans et la variation de la température de l’air et de la surface des océans dans la région des îles Marquises. J’ai mis les graphiques ici.
https://www.facebook.com/photo/?fbid=2170759756412341&set=a.360981180723550
Merci pour cette observation très pertinente.
C’est bien le même décalage que l’on observe sur les graphiques que vous mentionnez.
Le calcul de la corrélation croisée entre la température de surface océanique dans la région des îles Marquises et l’irradiance totale solaire le confirme.
Ce décalage est dû à l’effet intégrateur de l’océan. L’intégrale d’un sinus est égale à un cosinus qui n’est autre que le sinus décalé du quart de sa période.
C’est exactement ce que l’on observe.
L’évolution de la température de surface océanique contient donc la signature de l’activité solaire.
A titre d’information, voici l’avis de l’AFP Belgique, et la réponse du mathématicien Benoît Rittaud :
https://factuel.afp.com/doc.afp.com.327U8QT
https://mythesmanciesetmathematiques.wordpress.com/2022/04/14/panique-a-lafp/
Vous écrivez : « L’objectif du GIEC est de limiter l’exploitation des ressources terrestres et d’imposer un agenda politique non démocratiquement choisi sous le prétexte d’une soi-disant urgence climatique qui dépasse les souverainetés nationales. »
Plein de pays, notamment au sud, ne cessent de critiquer cette perte de souveraineté au niveau énergétique mais la doxa est si forte en occident qu’il n’en ait jamais fait allusion dans les médias. Le Nord se gargarise toujours de sauver l’humanité même quand il promeut des idéologies régressives. On l’avait vu avec avec d’autres idéologies passées.
Le Nord s’est développé grâce aux énergies fossiles et il dit maintenant aux pays du sud de ne pas les utiliser ! Dans cet esprit, GreenPeace, fer de lance idéologique, menace même d’attaquer en justice les pays du sud s’ils ne réduisent pas leur GES après avoir signé les accords de Paris.
C’est hélas dans la continuité historique de la volonté du Nord de régenter les conditions du développement des pays du sud mais ces politiques de développement restent injustes et régressives.
Bravo pour votre article.
En rajoutant que ni la Chine, ni l’Inde, ni la Russie ne tomberont dans le panneau, et feront tout pour profiter de la bêtise du monde occidental en la matière
Disons que plutôt ils suivront la même voie pour des raisons de raréfaction et par conséquent du coût des ressources. Et je pense que la Chine sera le premier pays à » réellement » suivre la voie de la décarbonation énergétique. Tout simplement pour des raisons économiques. Mais comme nous disons en Ardenne belge ; Avec tout ça ,on est pas rendu. Pas sur le plan des émissions. Mais sur le plan de la voie tracée par la plus grande escroquerie politique du 20ème siècle. Qui est la création du GIEC.
Article salutaire. J’ai du mal à comprendre comment la température moyenne de l’atmosphère terrestre de la Terre qui n’est que la mesure de la vitesse moyenne de translation des molécules la composant (selon 1/2 mv2 = 5/2kT) pourrait être réchauffée de plusieurs degrés par l’absorption du rayonnement IR par les molécules de CO2 aux pics de 4,5 et 15µ qui font vibrer les 2 atomes d’oxygène longitudinalement ou en torsion de part et d’autre de l’atome de carbone à l’intérieur de chaque molécule de CO2. Pour que cette énergie de vibration puisse être transférée aux autres molécules de gaz, il faudrait des chocs inélastiques entre molécules qui ne sont possibles que si les molécules sont beaucoup plus distantes les unes des autres qu’elles ne sont dans la basse et moyenne atmosphère ; ceci ne devient possible qu’à des pressions très faibles qu’on ne rencontre qu’à des dizaines de kilomètres d’altitude.
In fine au delà de l’irradiance solaire, n’est-ce pas la variation du champ magnétique solaire plus importante que l’irradiance qui faisant varier les doses de rayons cosmiques reçues par l’atmosphère jouent fortement sur la formation des noyaux de condensation et donc des nuages? (hypothèse et expériences de Svensmark)
Réponse à la première partie du commentaire.
La conversion de l’énergie de vibration du CO2 en énergie cinétique de translation des molécules de N2 et O2 pourrait-elle avoir un effet sur la température moyenne des basses couches atmosphériques ?
Considérant la Terre comme un corps noir à 15°C on trouve en intégrant l’équation de Planck de 14 à 16 µm, domaine d’absorption du CO2, que 9,3 % du rayonnement thermique de la Terre sont émis dans cet intervalle de longueurs d’onde. Le CO2, quels que soit son coefficient d’absorption et sa concentration, ne pourrait donc absorber au maximum que 9,3 % du rayonnement thermique de la Terre (représentant 21 % de l’énergie totale reçue du Soleil au sommet de l’atmosphère) soit un peu moins de 2 % de 342 W m-2 donc environ 7 W m-2 .
La conversion de l’énergie de vibration du CO2 en énergie cinétique de translation des molécules de N2 et O2 ne peut résulter que de chocs inélastiques car dans un choc élastique l’énergie interne de chaque molécule est conservée. La proportion de 0,001 % de chocs inélastiques peut être déduite de la référence (4) de http://www.science-climat-energie.be/2019/02/14/le-rechauffement-climatique-dorigine-anthropique/. Le nombre de collisions étant de 7 10^9 s-1 pour les molécules atmosphériques à la surface terrestre le nombre de chocs efficaces est réduit à 7 10^4 s-1 mais reste très important tenant compte de la durée de vie radiative du CO2 (0,4 s)
Pour estimer l’effet de cette conversion sur la température des basses couches atmosphériques il faudrait connaître le volume d’air dans lequel cette énergie sera dissipée. En utilisant la relation de Beer-Lambert log Io/I = A C L et en introduisant les valeur A = 20,2 m2/mol pour le coefficient d’absorption molaire du CO2 et C = 1,78 10-2 mol m-3 (pour 0,04 % de CO2 en volume) on trouve que log Io/I vaut 3 (99,9 % d’absorption) pour une épaisseur atmosphérique L = 8 m. Connaissant (loi des gaz parfaits) le nombre de molécules dans une colonne d’air de 8 m de hauteur et de 8 m3 de volume dans lequel seraient dissipés 7 W on trouve que l’énergie cinétique moyenne (5/2 kT) des molécules N2 et O2 n’augmenterait en une seconde que d’environ 0,0001 %. Cette valeur ne sert qu’à fixer un ordre de grandeur car il n’y a évidemment pas d’accumulation d’énergie cinétique au cours du temps puisqu’un important courant de convection existe déjà. Le gradient de température existant déjà dans les basses couches atmosphériques ne sera donc PAS affecté par la présence de CO2.
Réponse à la deuxième partie du commentaire.
L’irradiance solaire et l’effet Svensmark travaillent dans le même sens. Ce dernier n’est pas quantifiable dans le modèle thermique utilisé, et il est dès lors impossible de déterminer la part relative de ces 2 actions. L’irradiance solaire pourrait donc n’être que le proxy de la somme d’autres phénomènes, sans que cela n’ait d’impact sur les résultats des analyses.
Dans votre second paragraphe, vous invoquez le « calculateur en ligne de la chimie carbonatée de l’eau de mer, publié par l’Université du Colorado ».
Ce calculateur met en jeu, non seulement l’évolution de la température, mais également celle de l’alcalinité et du DIC (Total inorganic carbon).
On connaît assez bien l’évolution dans le temps de la température, mais comment connait-on celle des 2 autres facteurs ? Et quelle en est la cause ? Ou alors, quelque-chose m’aurait échappé ?
Nota : je fais la même critique à Camille Veyres, qui est un adepte de cette théorie (voir https://veyres48.monsite-orange.fr/page-5e3c39bc8373e.html, et en particulier ses slides 20 …).
L’onglet « Chemistry » du calculateur (https://biocycle.atmos.colostate.edu/shiny/carbonate/)
contient des références qui permettraient peut-être d’en savoir plus, sinon, il serait préférable de poser la question à ceux qui ont mis ce calculateur au point et qui sont incontestablement plus qualifiés dans ce domaine.
Nous avons simplement considéré une évolution linéaire des 3 facteurs entre leurs valeurs initiale (Scenario Preindustrial) et finale (Scenario Modern), et confronté cette théorie avec les observations.
En ajustant le relevé du CO2 à Mauna Loa pour tenir compte des émissions anthropiques d’une manière qui respecte les contraintes d’abondances isotopiques sur le delta_13C et le DELTA_14C, nous ne faisons que constater qu’il y a un excellent accord entre les observations et la théorie du calculateur, y compris les valeurs de ses paramètres.
Bonjour,
Votre raisonnement ne me convainc pas vraiment.
La loi de Henry dit :
« A température constante et à saturation, la quantité de gaz dissous dans un liquide est proportionnelle à la pression partielle qu’exerce ce gaz sur le liquide. »
Si les océans dégazent en raison de la température, alors le CO2 augmente dans l’atmosphère, et donc il doit également augmenter dans l’eau.
Bien à vous.
La loi de Henry stipule qu’à température constante la solubilité d’un gaz dans l’eau est proportionnelle à sa pression partielle dans l’atmosphère en contact. On peut l’écrire sous la forme : x (fraction molaire) = K . P (pression partielle).
A 15° C, avec 400 ppmv de CO2 dans l’air à la pression de 100 kPa, la pression partielle de CO2 est 4 10-4 kPa et x = 3,3 10-9 dans l’eau.
D’autre part, la solubilité d’un gaz dépend aussi de la température. K varie selon e^(- ΔH /RT) et la transformation du CO2 gazeux en CO2 dissous étant exothermique (ΔH = – 20 kJ/mol) K et la solubilité diminuent lorsque la température augmente. Un graphique Excel en 3 D permettrait de visualiser la situation lorsque à la fois la pression partielle et la température varient
Il faut remarquer que :
1°la solubilité varie linéairement avec la pression partielle mais exponentiellement avec la température.
2°les lois de la thermodynamique ne s’appliquent qu’à des situations d’équilibre, ce qui est rarement le cas pour le climat.
La solubilité diminue lorsque la température augmente, mais la pression partielle du CO2 dans l’atmosphère aussi. D’autre part, si j’utilise le calculateur en ligne mentionné dans l’article (https://biocycle.atmos.colostate.edu/shiny/carbonate/), que je me place dans le scénario « Preindustrial », il faut augmenter la température d’un peu plus de 10 degré pour passer de 263.5 ppm à 400 ppm, ce qui indique clairement que l’augmentation du CO2 ne peut être uniquement due à la température.
Dans un système air-eau à l’équilibre si la solubilité du CO2 dans l’eau diminue, la pression partielle du CO2 dans l’air doit nécessairement augmenter sinon où irait le CO2 libéré ? Le calculateur que vous mentionnez fait intervenir trois variables considérées comme indépendantes dans la phase aqueuse : l’alcalinité, la teneur totale en carbone inorganique dissous et la température. En jouant sur ces différentes variables on peut obtenir un vaste choix de valeurs finales pour la salinité, le pH ou la pression partielle en CO2 à l’équilibre mais cela a-t-il un sens physique ? Pour reprendre l’expression utilisée dans un de vos précédents commentaires : votre raisonnement ne me convainc pas vraiment.
C’est justement bien là qu’est le problème : si vous êtes contraint de faire varier ensemble, et à la hausse, les 3 paramètres (alcalinité, teneur totale en carbone inorganique et température) pour expliquer le passage de 280ppm à 400ppm du CO2 atmosphérique, alors la thèse défendue par cet article ne tient que si la température influence aussi les deux autres paramètres. Or, comme vous l’avez dit, ces trois paramètres sont sensés être indépendants. Je comprends pas non plus comment une augmentation du DIC est possible si les océans « dégazent ». Merci pour votre patience.
Je ne suis pas l’auteur de l’article auquel vous vous référez. Mes commentaires ne portent que sur :
1° la solubilité du CO2 dans l’eau en fonction de la pression partielle du gaz (loi de Henry) et de la température
2° la difficulté d’interpréter les résultats d’un calculateur pour un système multivariable
Réponse à Stéphane
Par Roland Van den Broek et Henri Masson
19 juillet 2022
Vu plusieurs formules mathématiques ne pouvant facilement être intégrées dans la ‘rubrique commentaire’, un .pdf de la réponse est disponible sur le site de SCE par le lien suivant:
https://www.science-climat-energie.be/wp-content/uploads/2022/07/reponse-CO2_rvdb_hm.pdf
Donc, dans ce document PDF, vous supposez que la température à un effet sur l’alkalinité et sur le DIC. Et en particulier, que quand la température augmente, le DIC augmente. C’est bien cela ? Comment expliquez-vous cela ? Intuitivement, sans apport externe, le DIC devrait diminuer s’il y a dégazage ? (C’est le fameux principe des vases communiquant.)
Le calculateur en ligne fournit les valeurs de TA, T et DIC pour les scénarios Preindustrial et Modern.
Dans un espace à 3 dimensions TA, T et DIC, nous disposons de 2 points correspondants à chaque scénario et supposons que l’évolution entre les 2 scénarios a suivi la droite entre ces 2 points, ce qui revient à considérer qu’il y a un couplage linéaire entre les 3 variables au cours de l’évolution entre les états Preindustrial et Modern.
Si s est un paramètre compris entre 0 et 1, et si les indices 0 et 1 correspondent respectivement aux états Preindustrial et Modern, l’équation paramétrique de cette droite prend la forme suivante :
TA(s) = s * (TA1 – TA0) + TA0
T(s) = s * (T1 – T0) + T0
DIC(s) = s * (DIC1 – DIC0) + TA0
ou de manière équivalente :
s = (TA(s) – TA0) / (TA1 – TA0) = (T(s) – T0) / (T1 – T0) = (DIC(s) – DIC0) / (DIC1 – DIC0)
Si l’on fixe une des variables, on peut en déduire s et calculer ensuite les 2 autres variables. Ceci ne préjuge en rien d’un effet de causalité d’une variable par rapport aux 2 autres, la seule hypothèse qui est faite est celle d’un couplage linéaire entre les 3 variables.
En donnant à s quelques valeurs uniformément réparties dans l’intervalle [0,1], on peut calculer les valeurs de TA, T et DIC au moyen des formules précédentes et injecter ces valeurs dans le calculateur en ligne pour en déduire la pCO2.
Il n’y a rien d’intuitif dans la chimie carbonatée de l’eau de mer qui est régie par un système de 6 équations non linéaires à 6 inconnues, et il est assez surprenant de constater qu’en faisant les calculs décrits ci-dessus, on obtient une relation linéaire entre le log de la pCO2 et la température, comme dans la loi de Henry.
Le choix des valeurs de TA, T et DIC des scénarios Preindustrial et Modern n’est pas détaillé dans le calculateur en ligne. Les références citées dans l’onglet chemistry du calculateur permettraient vraisemblablement d’en savoir plus, mais la matière est terriblement compliquée et nous ne pouvons que nous en remettre à l’expertise des auteurs du calculateur.
Je vais poser une question qui apparaîtra peut-être naïve aux yeux des grands scientifiques intervenant sur ce site, mais bizarrement, je n’ai trouvé nulle part d’explications sur le fait que, si la longueur d’onde du rayonnement infrarouge renvoyé par la terre est vraiment d’environ 10 micromètres, comme c’est généralement admis, comment la molécule de CO2 fait-elle pour capter ce rayonnement et le réémettre vers la terre alors que son opacité à l’infrarouge se situe pour une petite partie autour de 4 micromètres et pour le reste entre 14 et 16 micromètres ? Si quelqu’un a une réponse, j’ai soif d’apprendre !
Merci pour votre commentaire et félicitations pour votre soif de connaissance.
Tout corps à une température supérieure au zéro absolu émet un rayonnement thermique qui peut être décrit par l’équation de Planck (fig.1 de http://www.science-climat-energie.be/2018/04/26/du-bon-usage-de-la-formule-de-stefan-boltzmann/ ). Quelques exemples sont aussi présentés sur la fig. 1 de http://www.science-climat-energie.be/o2020/12/11/leffet-de-serre-et-le-bilan-energetique-de-la-terre/ . Ils montrent que l’intensité dépend de la température (équation (1), relation de Stefan-Boltzmann) et que le maximum d’émission peut être prévu par l’équation (3) (loi de Wien).
Si on considère la Terre comme un corps noir à 15°C (288 K) le rayonnement thermique émis présentera un maximum d’intensité à 10 µm (loi de Wien) mais le spectre s’étendra sur un large domaine de longueur d’onde : 95 % du rayonnement seront émis entre 5 et 40 µm. Le CO2 présente un zone d’absorption entre 14 et 16 µm avec un maximum à 15 µm (fig.5 de la dernière référence). En intégrant l’équation de Planck dans le domaine d’absorption du CO2 de 14 à 16 µm on trouve que 10 % seulement de l’énergie du rayonnement thermique de la Terre sont émis dans cet intervalle de longueurs d’onde. Le CO2, quelle que soit son abondance, ne pourra donc absorber plus que cette fraction du rayonnement thermique de la Terre. De plus, ce rayonnement absorbé ne sera PAS réémis vers la Terre car dans les basses couches atmosphériques la désactivation par collisions avec les molécules environnantes N2 et O2 est le mécanisme prépondérant. L’effet de serre radiatif, hypothèse de base de la théorie du réchauffement climatique d’origine anthropique, est sans fondement scientifique.
Il y a 60 millions d’années la température moyenne était beaucoup plus élevée qu’aujourd’hui. A tel point que des forêts tempérées étaient présentes au-delà du cercle polaire arctique. Au cours de ces 60 derniers millions d’années la température moyenne à la surface de la Terre n’a cessé de baisser pour aboutir à une succession de périodes glaciaires alors même que le soleil devient plus chaud au cours du temps (sauf erreur de 7% par milliard d’années).
Quelle est votre explication de cette baisse de température?
Effectivement la température a chuté au cours du Cénozoïque, depuis 66 millions d’années. Cette chute n’a pas été linéaire, loin s’en faut, elle est entrecoupée de périodes très chaudes (avec de nombreux ‘Optimas Climatiques’, exemples = Maximum Thermique Paleocene-Eocene ou ‘PETM’ (voir ci-dessous) …, Optimum Climatique Miocène moyen, etc.) alternant avec des périodes froides (exemple transition Eocene-Oligocene avec une baisse de la température de 5 à 7 °C …). . Le Cénozoïque a ainsi connu dans sa partie inférieure, donc plus ancienne, de nombreuses oscillations climatiques avec souvent des températures bien supérieures (> 10°C) à celles d’aujourd’hui (cf. PETM in https://www.science-climat-energie.be/2019/04/27/evenements-hyperthermiques-du-tertiaire-precurseurs-de-la-situation-actuelle/). Le refroidissement l’emporte finalement, avec le développement d’abord de l’inlandsis antarctique il y 34 Ma, puis arctique vers 3,2-2,7 Ma, dans la deuxième partie du Cénozoïque (plus récente).
Le Cénozoïque fait suite au Mésozoïque, longue période chaude, sans glaciations, avec des températures élevées. Durant le Cénozoïque de nombreux événements ont eu lieu : surtout une forte activité tectonique (surrection de l’Himalaya, des Andes, des montagnes Rocheuses, formation de l’Isthme de Panama … etc), changement des circulations océaniques, perturbations des cycles biogéochimiques notamment à travers la préservation de la matière organique dans des bassins sédimentaires très subsidents (= bassins anoxiques de la Mer Caspienne, de la Mer Noire …), évolution des plantes (surtout angiospermes).
Ces événements ayant leur propre fréquence brouillent le signal de l’évolution de la température. Cette dernière est ainsi interprétée de différentes manières, par exemple il est souvent question de la baisse du taux de CO2 suite à l’érosion des silicates (= ‘pompe à CO2’) résultat de l’érosion des chaînes de montagnes (par exemple l’Himalaya). Cette interprétation basée sur l’hypothèse de l’effet de serre est contestée par de nombreux auteurs (cf. T. Cronin, 2009 in https://cup.columbia.edu/book/paleoclimates/9780231144940) qui mettent l’accent sur la variation du forçage astronomique (cf. cycles de Milankovitch) modifiant périodiquement la distribution de l’insolation solaire. D’autres estiment que c’est la dérive des continents et l’évolution de leur relief qui modifient le transfert de chaleur de l’équateur vers les pôles, suite à un changement de la dynamique atmosphérique et océanique (exemple https://www.science-climat-energie.be/2020/05/22/arctique-geologique-1-2/).
Le refroidissement cénozoïque est ainsi conditionné en premier lieu par la tectonique et le forçage océanique qui en résulte. Les cycles Dansgaard-Oescger pléistocènes montrent l’importance du forçage océanique, les fortes variations de température ne peuvent pas s’expliquer par le ‘bouton CO2’ (cf. mon, commentaire ici : https://www.science-climat-energie.be/la-temperature-moyenne-de-latmosphere-entre-1880-et-aujourdhui/#comment-21663. Le forçage océanique est in fine sous le contrôle de l’activité interne du globe, il est modulé par le forçage astronomique (par exemple les maxima d’englacement pour une configuration donnée des masses continentales sont en relation avec l’obliquité (41 ka) en haute latitude (B. Van Vliet, 2013, https://www.fr.fnac.be/a5152633/Brigitte-Van-Vliet-Lanoe-Cryosphere.)
Il est impossible d’aller plus loin ici dans un commentaire, il faut considérer chaque oscillation climatique pour elle-même, mais le Cénozoïque nous montre que le changement climatique est la règle en géologie (cf. https://www.science-climat-energie.be/climat-et-geologie/le-changement-climatique-la-regle-en-geologie/) et surtout qu’il est multifactoriel et que la température a souvent varié dans des fourchettes bien supérieures par rapport à la température d’aujourd’hui. Seules de meilleures résolutions stratigraphiques (= temporelles) permettront d’établir la part des phénomènes impliqués et leurs successions précises.
Pour terminer d’’où viennent les 7% par milliard d’années que vous mentionnez ? Ce point remonte bien loin dans le temps, en dehors de la fenêtre temporelle prise en considération dans votre commentaire.
Bonjour, je vais reprendre le commentaire de Mr Dumon :
Je vais poser une question qui apparaîtra peut-être naïve aux yeux des grands scientifiques intervenant sur ce site, mais bizarrement, je n’ai trouvé nulle part d’explications sur le fait que, si la longueur d’onde du rayonnement infrarouge renvoyé par la terre est vraiment d’environ 10 micromètres, comme c’est généralement admis, comment la molécule de CO2 fait-elle pour capter ce rayonnement et le réémettre vers la terre alors que son opacité à l’infrarouge se situe pour une petite partie autour de 4 micromètres et pour le reste entre 14 et 16 micromètres ? Si quelqu’un a une réponse, j’ai soif d’apprendre !
Quelqu’un peut y répondre.
Merci
Bonjour,
Le rayonnement infra-rouge renvoyé par le sol vers l’atmosphère n’est pas composé uniquement de rayonnements à 10 micromètres. La Terre renvoie tout un spectre de rayonnements vers l’espace, compris entre 2 et 50 micromètres. Pour avoir une idée des rayonnements émis par le sol à la température de 15°C vous pouvez considérer ce qu’un corps noir émet à cette température, en utilisant la loi de Planck. Voyez ce calculateur en ligne (écrivez 15°C et cliquez sur « calculate ») :
https://www.spectralcalc.com/blackbody_calculator/blackbody.php
Vous verrez qu’à 15°C un corps noir émet un spectre de rayonnements, dont le maximum est à 10 micromètres. Ce corps noir émet également bien les rayonnements captés par le CO2, entre 14 et 16 micromètres.
Maintenant, il est évident que la Terre n’est pas vraiment un corps noir, donc la vraie courbe sera un peu différente de la courbe en cloche calculée avec la loi de Planck.
Lea auteurs de cet article prétendent s’appuyer sur ‘une étude bien plus approfondie en cours de finalisation, qui sera publiée sous format PDF dans les prochaines semaines’, mais ne fournissent aucune référence. Idem pour les multiples graphiques intégrés à l’article. Que cela résulte d’un oubli ou d’un choix délibéré, il en ressort une impression de travail négligé.
Il me semble aussi important de signaler que les articles climatosceptiques, tels que celui abordé, sont fréquemment rédigés par des personnes qui ne possèdent pas d’expertise en climatologie ou en sciences atmosphériques. Cela inclut l’auteur de l’article en question, qui se présente comme un ingénieur civil, et pour lequel on ne trouve aussi aucune référence ou accréditation professionnelle sur le net. Ceci contraste fortement avec les rapports du GIEC, qui sont le fruit de collaborations entre des centaines de scientifiques spécialisés, de climatologues reconnus et d’experts de l’environnement du monde entier
À propos du GIEC, il me semble essentiel d’ajouter un élément concernant les rapports qu’il émet. Ces derniers sont rédigés par des auteurs internationaux qui synthétisent les articles scientifiques préalablement validés. Avant leur publication, les rapports font l’objet d’une révision par des experts scientifiques bénévoles. Les contributeurs aux rapports du GIEC sont en général des chercheurs renommés associés à des institutions académiques et de recherche. Leur contribution est souvent régie par des normes exigeantes en matière de déontologie scientifique. En outre, la procédure demande fréquemment une déclaration des conflits d’intérêts, ce qui garantit une transparence et une intégrité supplémentaires (difficile d’imaginer un quelconque lobby influençant les rapports). Pour illustrer, 136 706 commentaires ont été intégrés lors de la préparation du cinquième rapport. Le document final nécessite l’approbation unanime de tous les états membres, y compris ceux qui sont de grands exportateurs de pétrole. Toutes les publications du GIEC ont reçu une approbation unanime. Quant aux climatosceptiques, ils sont encouragés à présenter leurs arguments auprès du GIEC pour évaluation scientifique, cependant, rares sont ceux qui le font. Les auteurs de l’article critiquent ce qu’ils appellent les « modèles » du GIEC; cependant, le GIEC n’élabore pas de modèles. Au lieu de cela, cette organisation de renommée mondiale compile et synthétise la recherche scientifique déjà examinée par des pairs.
L’article original soutient que le soleil, et non le CO2, est la principale cause du réchauffement climatique. Cependant, les données scientifiques prouvent que l’activité solaire a été relativement stable ou a même diminué au cours des dernières décennies, alors que les températures terrestres ont continué à augmenter. Les variations solaires ne peuvent donc pas être la principale force derrière le changement climatique actuel. Ces affirmations sont étayées par des études de la NASA et d’autres organisations reconnues comme la WMO. (“For more than 40 years, satellites have observed the Sun’s energy output, which has gone up or down by less than 0.1 percent during that period. Since 1750, the warming driven by greenhouse gases coming from the human burning of fossil fuels is over 270 times greater than the slight extra warming coming from the Sun itself over that same time interval.”, cf. What Is the Sun’s Role in Climate Change? – NASA Science)
Les variations de température dans les différentes couches de l’atmosphère démontrent clairement que les gaz à effet de serre, et non les fluctuations solaires, sont responsables du réchauffement climatique actuel. Si le soleil était la cause, nous observerions un réchauffement global de toutes les couches de l’atmosphère. Cependant, les mesures indiquent un réchauffement de la troposphère (couche basse de l’atmosphère) et un refroidissement de la stratosphère (couche haute), ce qui est cohérent avec l’effet des gaz à effet de serre. (cf. les travaux réalisés par des équipes de chercheurs de renommée internationale, notamment en collaboration avec le Système de Télédétection de Californie et l’Administration nationale océanique et atmosphérique américaine (NOAA), et qui se sont déroulés sous la direction du climatologue américain Benjamin Santer).
L’article original prétend que les émissions de CO2 sont naturelles à 96%. Cela ignore les émissions anthropiques qui perturbent le cycle naturel du CO2. Bien que les échanges naturels de CO2 entre la biosphère (terrestre et océanique) et l’atmosphère soient importants, ils se sont compensés pendant des millénaires, maintenant des niveaux de CO2 atmosphérique stables. L’augmentation rapide du CO2 atmosphérique que nous observons aujourd’hui est la conséquence directe des émissions supplémentaires provenant des activités humaines
Bien que les océans émettent du CO2 lorsqu’ils chauffent, ce processus n’explique pas l’augmentation rapide de la teneur en CO2 atmosphérique depuis l’ère industrielle. Les preuves basées sur les isotopes montrent que la hausse marquée du CO2 résulte plutôt de la combustion des combustibles fossiles que de sources naturelles. En effet, grâce à l’analyse de la composition isotopique, les scientifiques parviennent à tracer l’origine du CO2. La présence accrue de CO2 atmosphérique appauvri en isotope C13 révèle une origine anthropique, spécifiquement la combustion de ressources fossiles. D’autre part, si la théorie voulant que l’augmentation de CO2 atmosphérique provienne essentiellement du réchauffement océanique était exacte, on s’attendrait à ce que les océans contiennent moins de CO2, étant donné qu’ils se réchauffent et en relâchent. Or, les observations scientifiques indiquent une acidification des océans, preuve qu’ils absorbent davantage de CO2 qu’ils n’en émettent.
La ‘version complète’ de l’article de mars 2022 a été annoncée en mars 2023. Elle est accessible à partir du lien suivant : Soleil, température et CO2 , version complète).
Vous faites fausse route en mettant les climatologues sur un piédestal. Un climatologue est un scientifique généraliste qui utilise des concepts de physique, de mathématique, d’informatique et de chimie. Un climatologue n’est pas chimiste, mathématicien, physicien, etc. Des problèmes fondamentaux de chimie-physique sont présents dans les modèles proposés par les climatologues. Référez-vous par exemple aux articles du professeur Geuskens, chimiste, pour vous en convaincre (ici). Il en va de même pour les mathématiques (problèmes dans les modèles, problème du chaos, etc.) (voir par exemple les articles de H. Masson, ici).
Quant au GIEC, il ne prend en considération que les publications qui l’arrange et son fonctionnement n’est pas aussi idyllique (ici).
Voyez également le rapport CLINTEL, écrit par des spécialistes comme Ross McKitrick (statisticien ayant démontré que certaines courbes présentées par le GIEC sont fausses), ou l’italien Nicola Scafetta, physicien, qui nous montre que les paramètres solaires sont négligés par le GIEC (ici).
Bref, enlevez vos œillères, lisez toutes les publications par vous-même sans passer par le rapport du GIEC, et faites fonctionner vos neurones.
Le travail négligé que vous évoquez est la synthèse d’une brique de plus de 140 pages qui contient une cinquantaine de références et dont les analyses sont entièrement basées sur les observations. Pour des raisons trop longues à expliquer, elle a été publiée plus tardivement que prévu. Vous la trouverez ici:
https://soleil-temp-co2.netlify.app/
Il y a environ 5 ans, lorsque j’ai instruit le dossier du changement climatique à charge et à décharge, je me suis rendu compte qu’il y avait un problème avec les cultistes du GIEC qui refusaient de participer aux débats sous prétexte que la science était établie.
Vous présentez le GIEC comme une organisation de coordination scientifique de haut niveau qui traite de tous les aspects du climat, mais vous n’avez vraisemblablement pas constaté que le GIEC ne s’intéresse qu’à l’impact de l’activité humaine sur le climat. C’est repris à l’article 2 de ses statuts. Pensez-vous réellement que le GIEC va prendre en considération des articles contraires à ses thèses ? N’oubliez pas non plus le climategate où les scientifiques qui gèrent les relevés de température ont été pris la main dans le sac à manipuler les données parce qu’elles contredisaient l’hypothèse de l’effet de serre atmosphérique.
Force est de constater que le GIEC est une organisation politique qui a pris le CO2 anthropique comme prétexte pour changer la répartition mondiale des richesses. Ses dirigeants ne s’en cachent d’ailleurs pas. Ce problème est sur la table, mais il y a vraisemblablement une meilleure solution que celle qui consiste à détruire l’économie de nos sociétés occidentales.
Le rayonnement solaire moyenné sur une centaine d’années n’a quasiment pas cessé d’augmenter depuis la fin du Petit Age Glaciaire.
https://soleil-temp-co2.netlify.app/02-base_data_new#sec-DB-ITS
L’activité solaire instantanée a effectivement diminué lors des derniers cycles solaires. C’est l’inertie thermique des océans qui explique que la température n’a pas encore diminué.
Les stations terrestres d’Uccle et de De Bilt ont observé une augmentation de 15% du rayonnement au sol au cours des dernières décennies.
https://www.meteo.be/fr/climat/changement-climatique-en-belgique/a-uccle/rayonnement-solaire/rayonnement-global
https://climexp.knmi.nl/plotseries.cgi?id=someone@somewhere&TYPE=qq&WMO=qq260_mean12_anom_50_runningmeanforwards&STATION=De_Bilt&NAME=mean_daily_global_radiation&KIND=yr0
Ceci n’empêche pas ces instituts météorologiques de produire des projections de température entièrement basées sur les scénarios apocalyptiques du GIEC (RCP).
Le réchauffement de la troposphère et le refroidissement de la stratosphère que vous mentionnez n’ont été relevés par satellite que sur une période bien trop courte pour en tirer des conclusions sur des évolutions à long terme.
Ce sont les chiffres publiés par le GIEC qui permettent de déduire que le flux de CO2 est à 96% naturel.
https://soleil-temp-co2.netlify.app/06-relation-co2-temp_new#sec-ConsCycleCarbGIEC
Nous considérons que la part anthropique du CO2 dans le relevé de Mauna Loa est d’environ 75%.
Cette valeur respecte les contraintes d’abondance isotopiques que vous évoquez.
https://soleil-temp-co2.netlify.app/06-relation-co2-temp_new#sec-Anal-CT4
https://soleil-temp-co2.netlify.app/06-relation-co2-temp_new#sec-Anal-CT5
Pour ce qui concerne l’acidification des océans, je ne connais pas de série temporelle du pH de l’eau de mer.
Ce sujet est traité sur ce site. Voici 2 liens.
https://www.science-climat-energie.be/2018/06/05/reflexions-sur-lacidification-des-oceans/ et
https://www.science-climat-energie.be/2022/03/04/la-plupart-des-etudes-exagerent-les-effets-de-lacidification-de-locean/
Il n’est pas nécessaire d’assimiler les 140 pages de la brique pour comprendre que le réchauffement observé est naturel.
D’autres arguments plus simples suffisent pour se convertir au climato-réalisme.
J’ai expliqué ma démarche dans un article publié en 2 parties.
http://www.science-climat-energie.be/2020/05/08/le-giec-lhypothese-du-co2-et-le-soleil-1-2/
http://www.science-climat-energie.be/2020/05/15/le-giec-lhypothese-du-co2-et-le-soleil-2-2/
J’espère que cela réveillera votre bon sens et votre esprit critique. C’est tout le bien que je vous souhaite.